现在多大的棋盘的围棋已经能穷举了？

5路棋盘已经被穷举了。

2002年，Erik van der Werf 在Compute Go的邮件列表中宣布，解决了5*5的围棋问题。其邮件内容如下:

昨天，我的程序解决了从中心第一步开始的5x5围棋问题。正如预期的那样，这是先手的胜利，得分为25分（整个棋盘归属于黑方）。
我使用了迭代加深的Alpha-beta搜索（PVS），并结合了以下技术：
- 置换表（2层替换方案，2 x 2^24条目）
- 增强的置换截断
- 在置换表中的对称性查找
- 2个关键走法
- 历史启发式
- 用于无条件活棋的本森算法（扩展到无条件领地）
- 对于本森算法未确定的位置进行启发式评估
解决方案在22层深度（对于空棋盘为23层深度）时找到。（在P4 2.0GHz上大约4小时搜索了4,472,000,000个节点）
我的搜索能够解决5x5问题的主要原因是本森算法，它将检测到全棋盘胜利的深度至少减少了6层（相比于我以前的实现，它需要进行许多操作）。
只使用了简单的（日本）劫争规则，因此结果与任何超级劫争规则无关。这并不意味着超级劫争不重要，只是从空的5x5棋盘上有一条强制路线可以避免所有长周期。

结论是黑先走在中央的话，可以吃尽白棋。比较有趣的是考察黑棋第一步走在2路的结果：

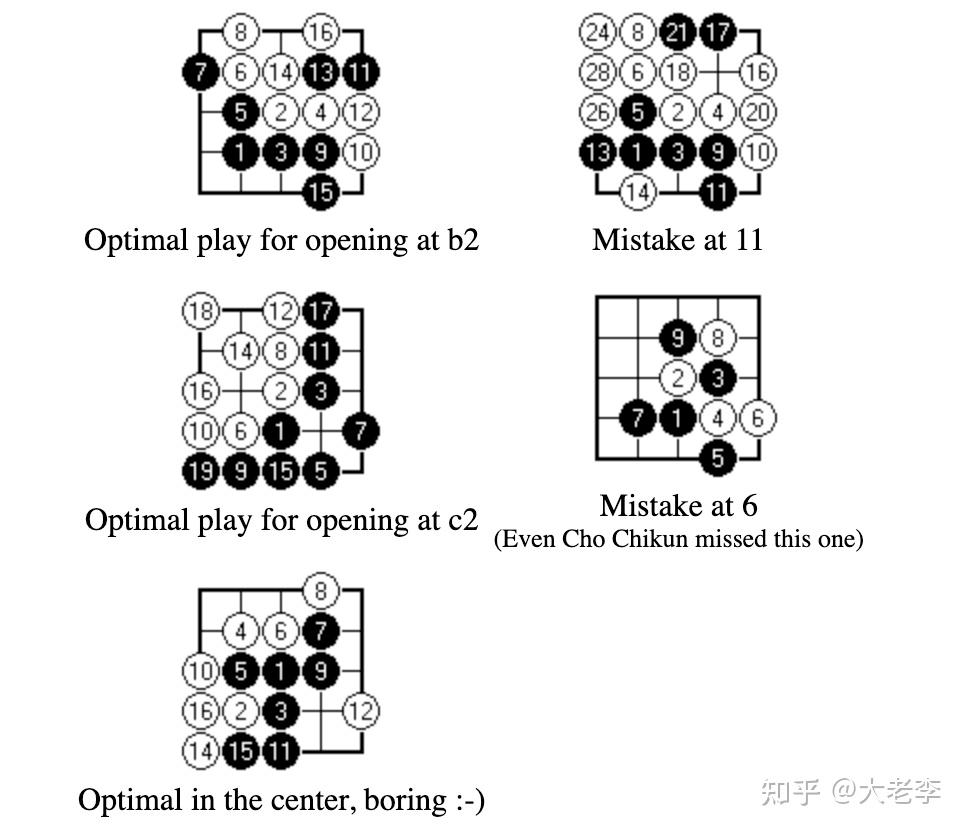
其中还包含一些赵治勋错过的下法。参考：5x5 Go is solved

6路围棋还没有被穷举过。

2015年，李喆六段曾宣布过解决了7路盘的围棋问题，但人脑计算无疑是有漏洞的。而且现在已经被AI找到了李喆错过的一些着法。可搜索公众号“鬼之一首”看详情。