这道多选题运用了蒙日圆性质的推广,对于A选项如何能快速判断出P点的轨迹方程以及k_3*k_4的值?
从 为定值,不易判断点
的轨迹。
为定值应是点
轨迹曲线的性质
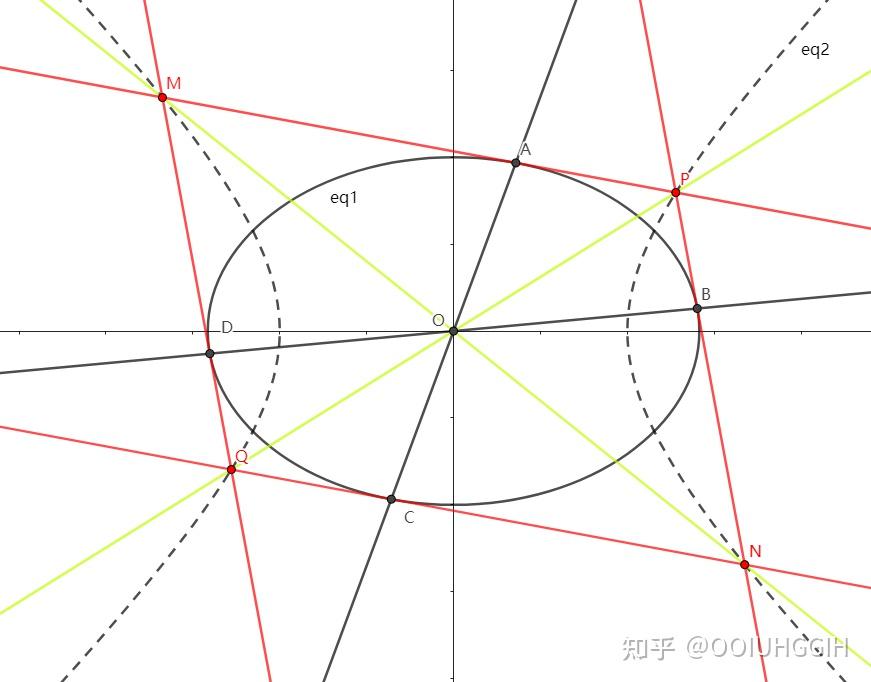
如图,延长直线 交椭圆于点
,延长
交椭圆于点
。
易证 ,则
,
,所以
,从而
四边形是椭圆的内接平行四边形。易证椭圆内接平行四边形
四个顶点的切线构成
椭圆的外切平行四边形 。
有心圆锥曲线的内接平行四边形的两组对边平行于圆锥曲线的一对共轭直径。共轭直径所在直线斜
率之积(斜率均存在)为定值。
设圆锥曲线的中心在坐标原点,曲线方程设为: ,两条直径
方程
分别为 。直线
关于
的极点:
直径 共轭,则直线
的极点在直线
上,于是
,直线
斜率之积
(图中
,直线
斜率之积
)
如果平行四边形 内接于一条圆锥曲线,则
平行于该圆锥曲线的一对共轭直
径,于是 为定值。
平行四边形 内接于一条圆锥曲线,即
在同一条圆锥曲线上,几何证法尚未想
到,代数证法如下。(证明 射影相关,则直线
包络一 条圆锥曲线,点
是直线
关
于椭圆的配极变换,点 的轨迹也是一条圆锥曲线)
设点
直线 是点
关于椭圆的极线,立即可得
的方程:
。与椭圆
联立有:
展开得
设 ,于是有:
可得点 的轨迹方程:
对于点 ,
对于点 ,
对于点 ,
同理可得轨迹方程:
所以点 在同一条圆锥曲线上,所以平行四边形
的邻边
平行于
的一对共轭直径
于是
代入参数 可得点
的方程:
由 ,可知直线
是点
上直线束对合的互逆直线对。二重元素是:
解得 ,即
和
是点
上对合的二重元素。由此可知
直线 重合,切线
重合,点
三点重合,点
的坐标
,此
时点 在椭圆上。当点
在椭圆内时,在实平面内不存在过点
的实直线与椭圆相切。于是点
在第一象限的轨迹范围是 (?)
点 在第一象限还应去掉一点
,因为点
上直线对合的互逆对,关于二重元素调和共轭
直线 的斜率满足方程:
于是可得: ,当
,
或
所以 是点
上对合的互逆直线对,此时
,
点 坐标
,可以验证点
的坐标满足轨迹方程,此时
斜率不满足题设要求
综上是点 在第一象限的轨迹范围是
,设
,
,
无最值
,设
,