光年是以光速运行一年的距离，但是根据（尺缩钟慢效应），以光速运行1光年的距离还需要一年吗？

以光速运行1光年的距离就是需要一年的时间，所谓的“尺缩钟慢”效应，只是一种因信息传递速度有限而导致的“观测效应”。

关于“尺缩钟慢”效应，可以这样理解：假设有两个观测者A和B，在同一原点（点O）处，以同样的速度反方向匀速行驶。在时空图中可以用下图来表示：

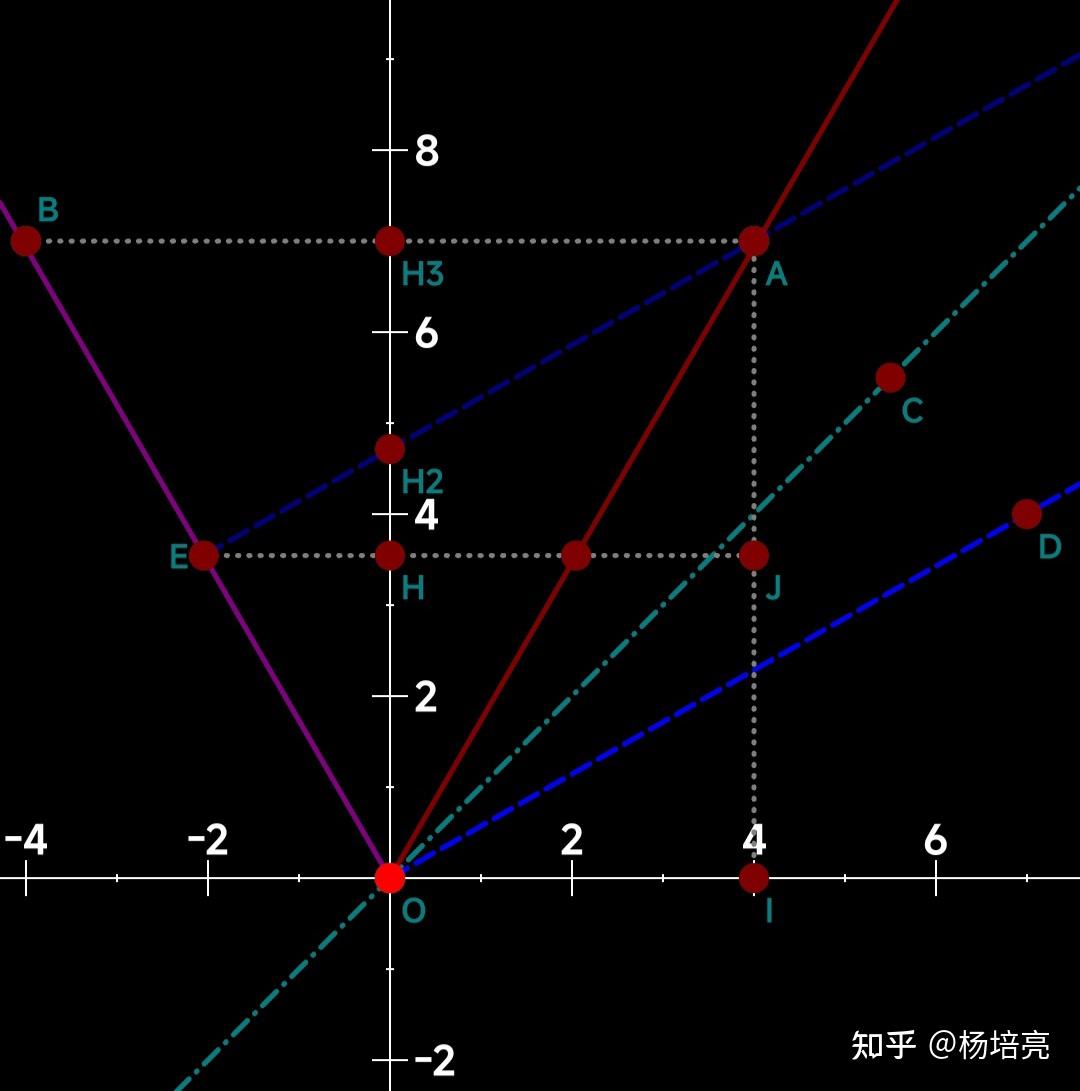
图一中：1、射线OA是观测者A感知的“时间线”；2、射线OB是观测者B感知的“时间线”；3、射线OD是观测者A感知的类空线；4、直线OC是观测者A方向的“类光线”；5、EA是与OD平行的、观测者A在A点时的“等时线”；6、点A与横轴做垂线，垂足为I；7、点E与AI做垂线，垂足为J。8、EJ与纵轴相交于点H，EA与纵轴相交于点H2，BA与纵轴相交于点H3。

按图中示意，在观测者A看来，E点与A点是“同时的”。也就是说，在观测者A看来，观测者A在A点时与观测者B在E点时是“同时的”。

再把观测者B看到的加在图上：

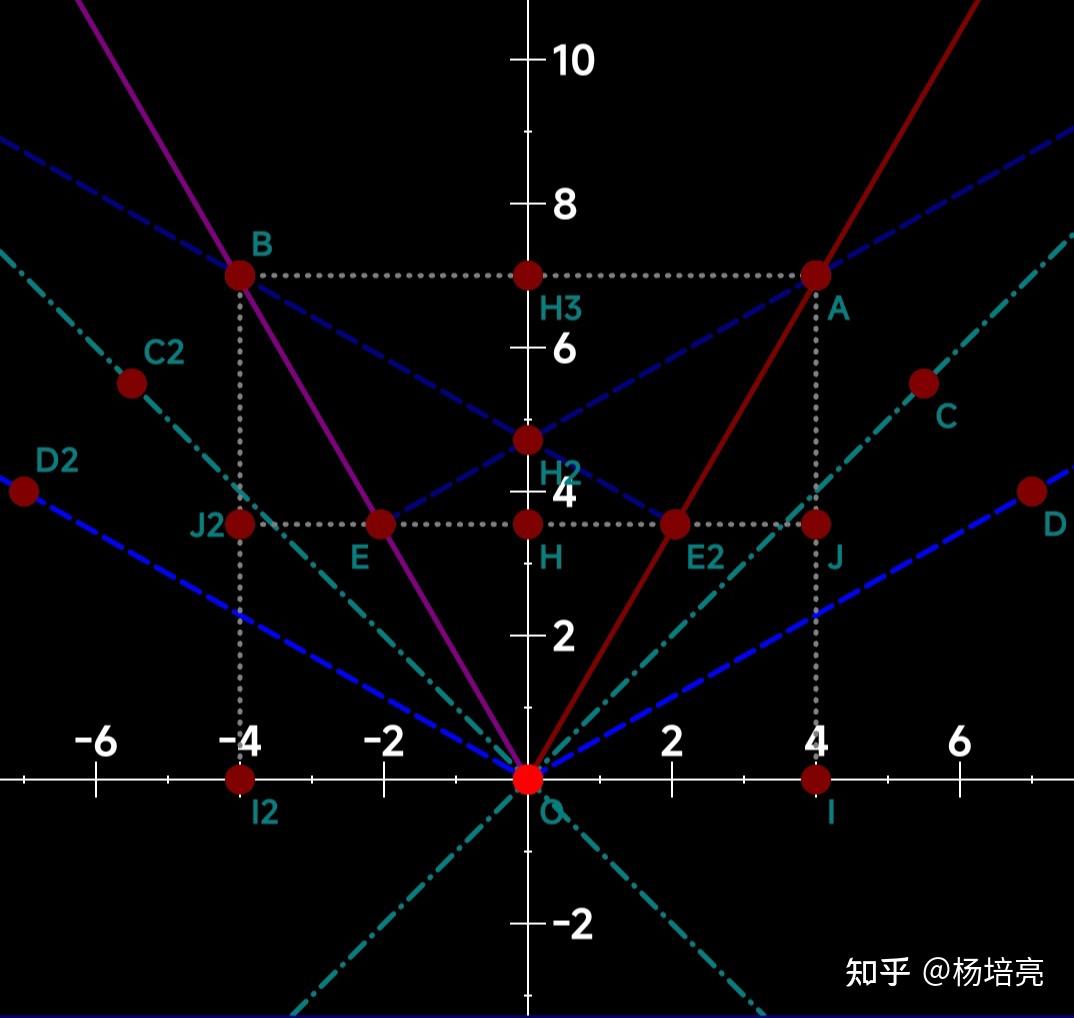
图二中：1、射线OC2为观测者B方向的“类光线”；2、射线OD2是观测者B感知的“类空线”；3、射线E2B为与OD2平行的、观测者B在B点时的“等时线”；4、点B与横轴做垂线，垂足为I2；5、点E2与BI2做垂线，垂足为J2。

这样，在观测者B看来，E2点与B点是“同时的”。也就是说，在观测者B看来，观测者B在B点时与观测者A在E2点时是“同时的”。

这就是所谓的“同时的相对性”。

在观测者A看来，观测者B在E点时与自己在A点时“同时”，是A的时间“变慢了”。而在观测者B看来，观测者A在E2点时与自己在B点时“同时”，是B的时间“变慢了”。那么，到底是谁的时间慢了？

答案还是在图中：当又有一个处于原点中的观察者O时，在O看来：A与B才是真正的“同时”——AI=BI2=H3O——谁的时间都没有变慢，这才是符合逻辑的“绝对的同时”。这个位于原点O的参考系，就是经典意义上的“绝对参考系”。这才是最符合逻辑的客观事实。

在这个“原点参考系（绝对参考系）”中，以光速运行1光年的距离，就只能是用了“一年的时间”。

在现实中，以现有的科技手段，无法找到这个“原点参考系”——所有的“原点”，都是在“运动中”——所以，只能是用“相对的参考系”来描述“看到的现象”。这样一来，观测者看到的都是不一样的——观测者A看到的，与观测者B看到的，就是“不一样的观测现象”——“同时的相对性”就成了“无奈中的妥协”。

在最后，我想说：虽然因为无法找到“绝对参考系”，而不得不使用“相对的参考系”，但不应该以此而否定“绝对参考系”的存在，因为“绝对参考系”在逻辑上是符合理性认知的。科学探索也同样是在尝试寻找“绝对参考系”，在大尺度宇宙学中，也有把“宇宙微波背景辐射”当做近似“绝对参考系”来使用的做法。拿时间来说，也是在尝试用各种算法，把“相对的同时”，尽可能统一为“同一的时间”，这不也是在尽可能的修正为“绝对的同时”吗？不然还对时干啥？各过各的时间得了呗。

在认识论中，怀疑论、独断论、不可知论、相对论，都是人类认识客观世界的阻碍，它们否认人有认识客观世界的可能——没有了各种“可能”，怎么还会有“希望”？