如果让你提名诺贝尔奖，你想提名哪位科学家？

从理论物理的本心出发，肯定是最希望M J Feigenbaum教授荣膺诺奖，但令人遗憾的是Feigenbaum教授于2019年不幸去世而再无可能。我想，如果Feigenbaum依旧在世，Feigenbaum和Parisi的组合（这个组合合理的授奖理由可以为“发展了非线性和复杂体系中的理论方法与数学技巧”等）或者Feiegnbaum+Albert Libchaber的组合（这个组合合理的理由可以是“对倍周期分岔中物理常数的认识”）都是合理的。

考虑到Parisi教授在2021年已经手握诺贝尔物理学奖，因此不妨期待一下法国物理学家Albert Libchaber（用法语是不是应该翻译为“利布沙贝”？啊，好吧）。

Albert Libchaber教授是一位视野开阔和兴趣广泛的学者（他的研究领覆盖了非线性和生物物理的许多分支领域。好吧，这也是非线性物理学者转战生物物理的又一缩影...）。1934年出生于巴黎（89岁...，如果有可能拿诺奖的话，最好快一点...），1965年获得巴黎大学物理学博士学位。

工作履历来看，Libchaber曾经供职于法国国家科学研究中心（CNRS，这里大抵是一个神人如云的机构，众多非线性物理大师盘踞此处...而且不少是独行侠...）和芝加哥大学，目前则是洛克菲勒大学的Detlev W. Bronk讲席教授^[1]。

Libchaber早年发明了能够在不干扰环境的情况下观察温度波动的方法。并通过这样的技术观察到实验层面的倍周期分岔现象，这也是Feigenbaum常数的实验证明。相关的实验最早在He4中实现^[2]，后续又在借助磁场获得额外自由度的Hg体系中再次实现^[3]。

这些实验是如此的完美，以至于它可以定量地测量表征级联到混沌的Feigenbaum常数。在Libchaber的实验之前，Feigenbaum的发现曾多次被拒绝发表，而Libchaber的工作完全扭转了Feigenbaum的困境（这个案例可以管窥理论先行的某些困境...）。

Libchaber于1986年与 Feigenbaum一起斩获Wolf物理学奖，Wolf基金会给出的评价是 "for his brilliant experimental demonstration of the transition to turbulence and chaos in dynamical systems(在动力系统中向湍流和混沌过渡的杰出实验演示)"。

后来，Libchaber的兴趣依旧在非线性领域，但是更多转向了生物物理^{[4] [1]}。

可以参见：1、Albert Libchaber的成果 2、Rockefeller大学关于Albert Libchaber教授的介绍

什么，如果你还不了解Feigenbaum常数 ，那我很推荐一篇文章，西门子（SIEMENS）公司推广数值软件Simcenter FLOEFD时请工程师Bornoff先生写的一篇短文^{[5] [6]}：

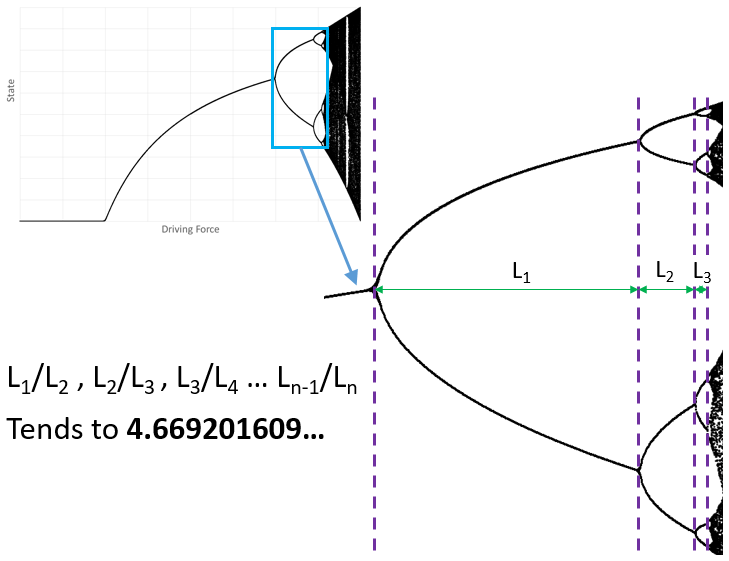
而Libchaber文章则提供了最早的实验证据^[2]

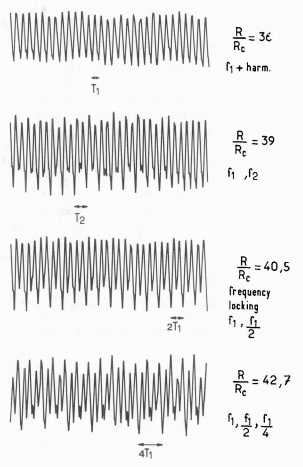
三二句题外话:

Bornoff先生是一名电子工程师，长期从事器件开发和仿真工作。相应的，他的教育经历也是落在工学领域。但是他在布鲁内尔大学第一次接触到Feigenbaum常数后便深感震惊，这种冲击感带来了他长期的努力，以至于29年后他借助供职企业SIEMENS的 Simcenter FLOEFD for NX来通过CFD 仿真观察二维 Rayleigh–Bénard模型中的Feigenbaum常数。

作为20世纪下半叶人类发现的唯一无量纲常数，其重要性不言而喻。和精细结构常数 以及Euler-Mascheroni常数 等无量纲常数一样，其可能存在惊人的普适性，稍有不同的是精细结构常数至少存在物理结构，而Euler-Mascheroni常数则至少存在数学解析。但是Feigenbaum常数依然如同黑暗法典一样，迷人、深邃并令人嗟呀不已。

也正因为无从下手，Feigenbaum常数的相关研究缓慢而冷淡。即使Feigenbaum和Libchaber凭借Wolf物理学奖证明了其价值（Wolf奖作为物理学界仅次于诺贝尔物理学奖的综合类物理学奖项，甚至充当了诺奖的显著风向标），但遗憾的是Feigenbaum常数从1978年诞生乃至随后四十年中相关的研究依然有限。

如同Bornoff先生一样，Feigenbaum常数吸引了无数的后来者（其中也包括我，也正因为如此我将硕士学位论文选题为此，并尝试提出了一种Feigenbaum常数对应的抽象物理图像），但是这条路依旧需要慢慢走。