绝大多数的数学难题在生活中是用不上的，为什么人们还在不断地探索和求解？

很多数学问题打一开始就不知道它们能在生活中有什么用。

这里我想引用刘慈欣《朝问道》里的一段对话：

图像定格，一声尖锐的鸣叫响起，排险者告诉人们，预警系统报警了。
“为什么？”总工程师不解地问。
“这个原始人仰望星空的时间超过了预警阈值，已对宇宙表现出了充分的好奇。到此为止，已在不同的地点观察到了十例这样的超限事件，符合报警条件。”
“如果我没记错的话，你前面说过，只有当有能力产生创世能级能量过程的文明出现时，预警系统才会报警。”
“你们看到的不正是这样一个文明吗？”

人类天生有一种好奇心和探索欲，这种内在驱动力也推动着人类持续进步，数学则提供了一种最纯粹、最理性的方法来实现这种追求。

然而这种追求真的是无用的吗？

以前也有很多类似的论调，比如「学数学没啥用，买菜难道还用得上微积分？」。但这完全是一个误导性的疑问，买菜也并非是衡量数学是否有用的标准。

许多看似毫无用处的数学理论，可能背后蕴藏着巨大的宝藏，等待被人类发掘的那一天，最终引发重大应用。这里我想举两个例子来做说明。

1. 黎曼几何与广义相对论

黎曼几何是 19 世纪德国数学家黎曼等人提出的，用于研究具有黎曼度量的光滑流形。他拓展了此前欧式几何的概念，是非欧几何的一种（另一种非欧几何是罗巴切夫斯基几何）。

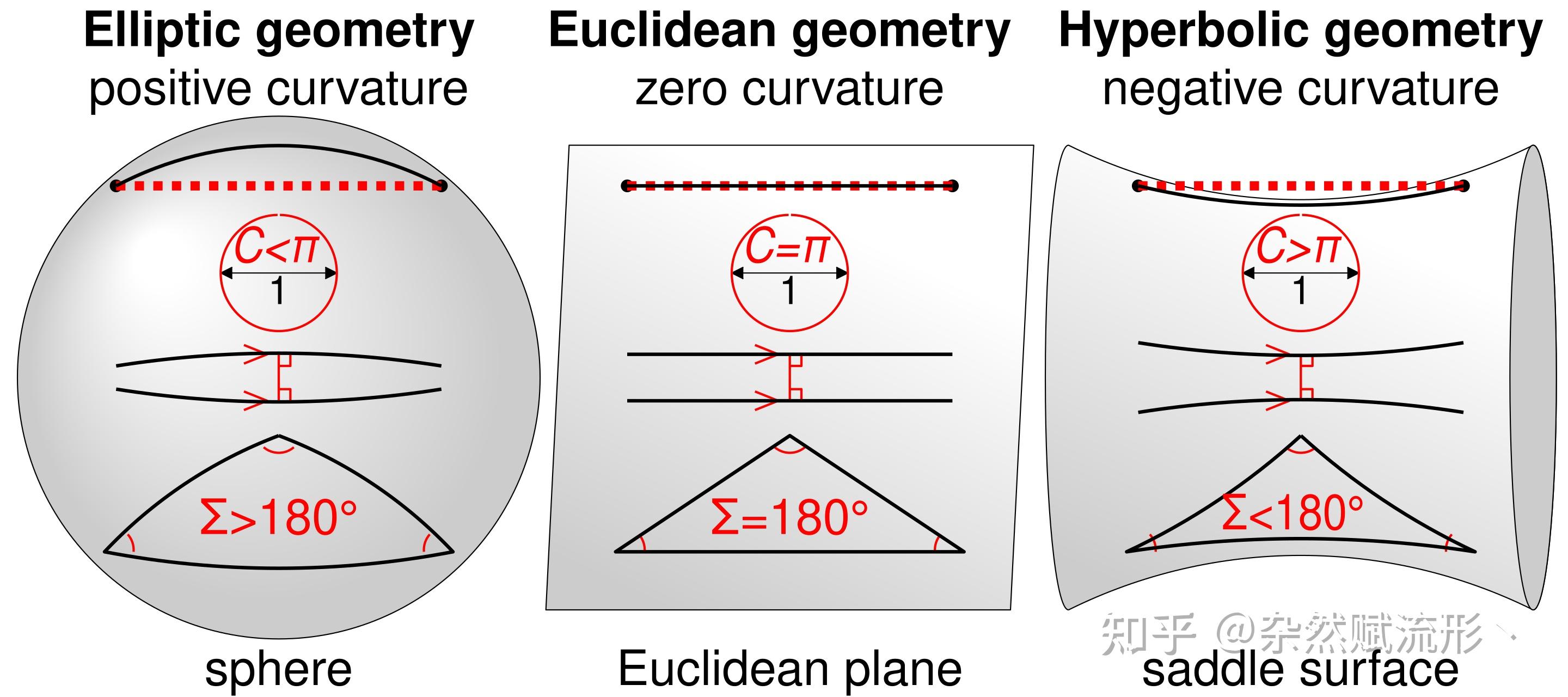
非欧几何最早源自古希腊数学家提出的第五共设——平行共设的证明上。部分数学家认为第五公设应该可以从其他四个公设出发而证明，由此成为一个定理，但一直没人成功。

争论了长达两千年，数学家们发现在假设第五公设不成立的前提下，反而能发展出一套自洽的理论，由此便逐渐诞生了非欧几何。如上图所示，在非欧几何中，三角形的内角和可以不等于 180°。

这一套几何理论有什么用呢？数学家们一开始也不知道。

直到 20 世纪初，爱因斯坦在建立广义相对论时，黎曼几何成了不可或缺的工具。广义相对论通过爱因斯坦场方程：

描述了时空与几何之间的关系。方程右边的 就是描述物质场的能量动量张量，而方程左边则是描述时空弯曲程度的纯几何量，其中 就是黎曼几何中的黎曼曲率张量。

值得一提的是，爱因斯坦一开始领悟到引力可以理解为时空的弯曲后，想要描述这种几何但苦于缺乏相应的数学工具。而正是爱因斯坦的大学同窗和好友格罗斯曼建议他学习黎曼几何，这才有了之后的广义相对论。

黎曼、高斯这一帮数学家当初在发展这套几何时显然不会意识到他们的理论能在一百年后大放异彩，广义相对论不仅完美解释了水星近日点进动等现象，还为黑洞、引力波等天文现象奠定了理论基础。

2. 数论和密码学

数论是纯数的分支之一，主要研究整数的性质，被称为「最纯」的数学领域。

高斯就曾说过：「数学是科学的皇后，数论是数学的皇后。」

按照大部分人的理解，数论就是最「没用」的数学领域，比如著名的哥德巴赫猜想：

任一大于 2 的偶数，都可以表示成两个素数之和。

这个猜想提出至今近 300 年，仍未得到解决，但依然吸引了许多数学家前赴后继地探索其证明。

像这种数论难题还有很多，它们不是和我们日常生活八竿子打不着吗？

但事实并非如此。

20 世纪以来，数论的成果在密码学中得到了广泛应用，尤其是基于素数分解的公钥加密算法，比如 RSA 算法，其核心思想就基于数论中的欧拉定理和模运算。

这套算法是 Ron Rivest, Adi Shamir 和 Leonard Adleman 于 1977 年发明的，它的安全性依赖于大整数分解的困难性，即在没有已知因数的情况下，极难将一个大整数分解为两个质数的乘积。

对于一个给定的整数 ，如果我们想将它分解为两个素数 ，即 ，已知的算法在计算上需要极高的资源，尤其是当 非常大时。但反过来我们已知其中一个因数 ，再去计算另一个因数 则是一个小学生都会的整数除法问题。

除了上述提到的 RSA 算法的例子外，还有椭圆曲线密码学、Diffie-Hellman 密钥交换等密码学应用，它们都和所谓的「最纯」的数学领域——数论密不可分。

3. 写在后面

数学的基础研究有时候需要长时间的积累，其成果往往并不是立竿见影的，而是为未来的科技和社会发展打下基础。我们无法预见某个数学难题未来会在什么领域产生深远影响，但这些「无用」的探索可能就是未来科技的基石。

从个人角度来说，面对难题也是一种自我挑战，就像攀登者渴望征服高峰一样，数学家也希望征服那些长期困扰人类智慧的难题。

但从整个人类历史来看，数学也是构建科学体系的基础，不断深入探索数学领域中的各个问题也能让我们的知识体系更加完整，推动科学的发展进步。

这里正摆着我——一个10岁的孩子——就能理解的问题，从那个时刻起，我知道我永远不会放弃它。我必须解决它。
——安德鲁·怀尔斯