中国首台仿星器测试平台取得重大成果，仿星器相比托卡马克是否更有希望实现可控核聚变？

发布时间：

2024-11-19 13:05

阅读量：

首先说结论：从经济角度，Tokamak方面光是ITER就投资了200亿欧元，在运行最大tokamak JT60SA投资5.6亿，以及各个主要聚变研究国家/初创的DEMO计划，包括CFETR、CFEDR、BEST、FAST、FNSF、KDEMO、ARC等等，数不尽的巨量资金与人员投入，都必须是首先实现可控核聚变的路线。这是历史的必然，是真正的大的要来了，是民心所向众望所归的。磁约束聚变的主要物理几乎都是基于tokamak研究的。没有极端的提速主要是因为能源似乎并不是真正的危机，又或者连天上顶着的那个聚变热源都没用明白。

之后谈谈仿星器Stellarator，尤其是CFQS（Chinese First Quasi-axisymmetric Stellarator), 核心概念是什么是Quasi-axisymmetric——准轴对称。

1. 托卡马克与仿星器的主要区分

在技术路线上，仿星器无疑是美的，从Spitzer通过扭转轴无电流构造旋转变换（即tokamak的安全因子）开始这一路线就非常巧妙，以至于许多原初的想法是现在某个理论的结果表达。开放系统，如磁镜，会使得粒子从两端开放的磁场中损失。简单的想法是使得磁镜首位闭合形成圆环，简单的首尾相连会造成许多问题：

磁力线随着环形装置径向长度由密到疏，径向产生 $\nabla B$ ，造成 $\nabla B$ 漂移
弯曲磁力线存在恒定曲率，产生曲率漂移
有限的平面圆线圈形成的磁面并非“甜甜圈”，磁面会在环向线圈间膨胀

在简单的环形位型中，所有约束带电粒子最终都会快速扩散出约束区域。磁力线如果能绕着磁面旋转，比如说时而在强场区、时而在弱场区、时而沿着大曲率路径、时而沿着小曲率路径，那么上述漂移就会被平均。如何令磁力线产生如上的旋转变换，可以通过一个简单的公式得出

$\iota=\frac{1}{2 \pi} \int_0^L \left[\frac{\mu_0 J}{2 B_0}-(\cosh \eta-1) d^{\prime}-\tau\right] \frac{d l}{\cosh \eta}-N$

中括号中的第一项是驱动等离子体产生电流以产生极向场，并与环向场叠加构造磁力线，例如tokamak。第二项表现为磁面截面的连续变换，比如说日本LHD仿星器。第三项为磁轴的扭转，比如Spitzer最初提出的仿星器。第二项与第三项构成了通过外部线圈结构形成的仿星器位形，第一项则是tokamak。

前者，1951年，Princeton University的Lyman Spitzer首先发明了利用外部磁场配置构造磁力线的装置——仿星器，并与PPPL开展了早期实验。但一直到1969年，在Model-C关闭的时候，都无法取得令人理想的限制作用。
后者，1958年，托卡马克T-1的相关工作由Natan Yavlinsky做出，并于1968年在T-3上获得了远远超过了当时其它约束设备取得的参数。1968年底，Model-C被关闭并随即改造为对称托卡马克，并高出了Model-C十倍以上的性能。

2. 准对称性

2.1 tokamak中的轴对称位形

由欧拉-拉格朗日方程：

$\frac{d}{dt}(\frac{\partial L}{\partial \dot{x}^j})=\frac{\partial L}{\partial x^j}$
若系统具有某种对称性，即 $\partial L/\partial x^j = 0$ ，则 $\frac{\partial L}{\partial \dot{x}^j}$ 与时间无关，构成守恒量，被称为Noether定理，构成连续对称性与守恒定理的联系。在轴对称场中，经典的如tokmaka，关于磁场的物理量在系统中是轴对称的，对于磁矢势满足：

$\frac{\partial}{\partial \phi}\{A_R,A_\phi,A_Z\} = 0$

对于规定磁场中的非相对论性带电粒子，柱坐标下Lagrangian写为：

$L(R,\phi,Z,\dot{R},\dot{\phi},\dot{Z},t)=q(A_R\dot{R}+A_{\phi}R\dot{\phi}+A_Z\dot{Z}) + \frac m2(\dot{R}^2+R^2\dot{\phi}^2+\dot{Z}^2)$

同样，对于轴对称情况， $\partial L/\partial \phi = 0$ 。Lagrangian对应的正则角动量为：

$p_{\phi} = \frac{\partial L}{\partial \dot{\phi}} = qA_{\phi}R + mR^2\dot{\phi} = qA_{\phi}R+mRv_{\phi}$

轴对称场中，正则角动量是守恒的，其中后一项为通常的角动量，受能量守恒的制约通常是有界的。前一项受到轴向磁矢势制约。也就是说，当令 $A_{\phi}$ 足够大时，可以认为粒子近似 $A_{\phi}R$ 是守恒的，即粒子被限制在固定的 $A_{\phi}R$ 平面上。考虑 $mRv_{\phi}$ 的有界性，即粒子的偏移也是有界的。同样可以证明，轴对称场中：

$\mathbf{B}\cdot \nabla(A_{\phi}R)=B_R\frac{\partial (A_{\phi}R)}{\partial R}+B_Z\frac{\partial (A_{\phi}R)}{\partial Z} = 0$

即 $\mathbf{B}$ 的场线与常数 $A_{\phi}R$ 表面相切，即与连续嵌套磁面一致。

对轴对称场通过安培定律：

$\mu_0 I = \oint \mathbf{B}\cdot dl$

对于环路积分项：

$\mathbf{B}\cdot dl = \frac{1}{R}[(\frac{\partial(A_{\phi}R)}{\partial R})^2+(\frac{\partial(A_{\phi}R)}{\partial Z})^{2}]^{1/2}d\mathscr{l} = \frac{|\nabla(A_{\phi}R)|}{R}d\mathscr{l} > 0$

即意味着轴对称位型必须需要具有环向电流。这与仿星器设计目标中要求的无等离子体电流相悖。

2.2 准对称性

描述磁流体位型，常用的方法是建立一套磁面坐标系。Boozer coordinates 可以被认为是一种直磁力线非正交磁面坐标系，协边与逆变形式可以表示为：
$\boldsymbol{B} = \nabla\psi\times\nabla\theta+\iota\nabla\zeta\times\nabla\psi$

$\boldsymbol{B}=I(\psi)\nabla\theta+G(\psi)\nabla\zeta+\beta(\psi,\theta,\zeta)\nabla\psi$
其中， $I(\psi)=B_{\theta}，G(\psi)=B_{\zeta}$ ，以表征环向电流与极向电流， $\beta$ 与比压相关。仿星器位型要求无等离子体电流下的平衡，即真空下也能够存在平衡位型，以此：真空下只具有磁面与环向场，因此：

$\boldsymbol{B} = G\nabla\zeta$

$\boldsymbol{B}\cdot\nabla{\zeta}=\nabla\psi\cdot\nabla\theta\times\nabla\zeta = \frac{B^2}{G}$

$\boldsymbol{B}\cdot\nabla{\theta}=\iota\nabla\psi\cdot\nabla\theta\times\nabla\zeta = \frac{\iota B^2}{G}$

粒子导心运动速度表示为 $v_{\parallel}\boldsymbol{b}+\boldsymbol{v}_d$

$\nabla B = \frac{\partial B}{\partial\psi}\nabla\psi+\frac{\partial B}{\partial \zeta}\nabla \zeta+\frac{\partial B}{\partial \theta}\nabla \theta$

在磁面径向上漂移为：
$\begin{eqnarray} \dot{\psi} &=& (v_{\parallel}\boldsymbol{b}+\boldsymbol{v}_d)\cdot\nabla\psi\\ &=& \boldsymbol{v}_d\cdot\nabla\psi\\ &=& \frac{m}{qB^3}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)\boldsymbol{B}\times\nabla B\cdot\nabla\psi\\ &=& \frac{m}{qB^3}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)(G\nabla\zeta)\times(\frac{\partial B}{\partial \theta}\nabla\theta)\cdot\nabla\psi\\ &=& -\frac{m}{qB}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)\frac{\partial B}{\partial \theta} \end{eqnarray}$
环向：
$\begin{eqnarray} \dot{\zeta} &=& (v_{\parallel}\boldsymbol{b}+\boldsymbol{v}_d)\cdot\nabla\zeta\\ &=& \frac{v_{\parallel}}{B}\boldsymbol{B}\cdot\nabla\zeta + \frac{m}{qB^3}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)\boldsymbol{B}\times\nabla B\cdot\nabla\zeta \\ &=& \frac{v_{\parallel}\cdot B}{G} \end{eqnarray}$
极向：
$\begin{eqnarray} \dot{\theta} &=& (v_{\parallel}\boldsymbol{b}+\boldsymbol{v}_d)\cdot\nabla\theta\\ &=& \frac{v_{\parallel}}{B}\boldsymbol{B}\cdot\nabla\theta + \frac{m}{qB^3}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)\boldsymbol{B}\times\nabla B\cdot\nabla\theta \\ &=& \frac{v_{\parallel}}{B}\frac{\iota B^2}{G} + \frac{m}{qB^3}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)(G\nabla\zeta)\times(\frac{\partial B}{\partial \psi}\nabla\psi)\cdot\nabla\theta \\ &=& \frac{v_{\parallel}\iota B}{G} + \frac{m}{qB}(\frac{v_{\perp}^2}{2}+v_{\parallel}^2)\frac{\partial B}{\partial \psi} \end{eqnarray}$
同时，动能与磁矩在导心运动时是守恒的，仅与磁场强度分布有关。
$v_{\perp}^2 = 2\mu B \\ v_{\parallel} = \pm\sqrt{v^2-2\mu B}$
综上，真空场下，导心轨道的 $\dot{\psi},\dot{\zeta},\dot{\theta}$ 只与磁场强度以及 $\iota(\psi)$ 有关。即粒子在磁场中导心运动只与磁面与磁场强度有关。此关系在非真空下依然成立，在此不做证明。此时，粒子的导心拉格朗日量表达为：
$L(\boldsymbol{x},v_{\parallel},\mu,\varphi,\dot{\boldsymbol{x}},\dot{v_{\parallel}},\dot{\mu},\dot{\varphi},t)= q\boldsymbol{A}\cdot\dot{\boldsymbol{x}}+mv_{\parallel}\boldsymbol{b}\cdot\dot{\boldsymbol{x}}+\frac{m}{q}\mu\dot{\varphi}-\frac{mv_{\parallel}^2}{2}-\mu B-q\Phi$
在Boozer坐标系中取规范（gauge）： $\boldsymbol{A}=\psi\nabla\theta-\psi_p\nabla\zeta$ 与位置变化 $\dot{\boldsymbol{x}}=\dot{\psi}\frac{\partial\boldsymbol{x}}{\partial\psi}+\dot{\theta}\frac{\partial\boldsymbol{x}}{\partial\theta}+\dot{\zeta}\frac{\partial\boldsymbol{x}}{\partial\zeta}$

代入Guiding-center Langragian表达式，可得：
$L(\boldsymbol{x},v_{\parallel},\mu,\varphi,\dot{\boldsymbol{x}},\dot{v_{\parallel}},\dot{\mu},\dot{\varphi},t)= q\psi\dot{\theta} -q\psi_p\dot{\zeta} +\frac{mv_{\parallel}}{B}(\dot{\psi}\beta+\dot{\theta}I+\dot{\zeta}G) +\frac{m}{q}\mu\dot{\varphi} -\frac{mv_{\parallel}^2}{2} -\mu B -q\Phi$
不难发现，Langragian只与 (a) $\psi,\psi_p,I,G$ （并且这些仅是磁面位置的函数）； (b)磁场的强度分布；（c) 静电势 $\Phi$ 有关。

回到Noether定理，假设在Boozer坐标 $(\psi,\zeta,\theta)$ 下，磁场与 $\zeta$ 无关，即 $B = B(\psi,\theta)$ ，构成了某种环对称，结合Noether定理，可以写出Boozer下在 $\zeta$ 上的守恒量：

$p_{\zeta}=\frac{\partial L}{\partial \dot{\zeta}}=-q\psi_p+\frac{mv_{\parallel}G}{B}$

此前提及的在轴对称场中的正则角动量 $p_{\phi}$ 是非导心的。将其变换为导心形式：
$\begin{eqnarray} p_{\phi} &=& qA_{\phi}R+mRv_{\phi}\\ &=& -q\psi_{p}+\frac mB \boldsymbol{v}\cdot(G\boldsymbol{b}-\boldsymbol{b}\times\nabla\psi_p)+const\\ &=& -q\psi_{p}+\frac{mG}{B} \boldsymbol{v}\cdot \boldsymbol{b}-\frac mB \boldsymbol{v}\cdot \boldsymbol{b}\times\nabla\psi_p +const\\ &=& -q\psi_{p}+\frac{mv_{\parallel}G}{B}-\frac mB \boldsymbol{v}\cdot \boldsymbol{b}\times\nabla\psi_p +const \end{eqnarray}$
其中， $\boldsymbol{v}\cdot \boldsymbol{b}\times\nabla\psi_p$ 在拉莫尔回转期间平均为0。与Boozer中的比较，产生了一致的形式。即在Boozer坐标系中的轴对称磁场描述具有和真实轴对称磁场具有一致的粒子约束形式。即使不存在等离子体电流，也能够产生与轴对称磁场位型一样的约束性能。

准对称性能够从上述论证中得出，当磁场强度分布分别与轴向、极向、螺旋方向无关时，粒子约束特性与真正对称系统一致，一般地被归类为

准轴对称(Quasi-Axisymmetry, QA) : $B = B(s,\theta)$
准极向对称(Quasi-Poloidal symmetry, QP): $B = B(s,\zeta)$
准螺旋对称(Quasi-Helical symmetry, QH): $B = B(s,M\theta-N\zeta)$

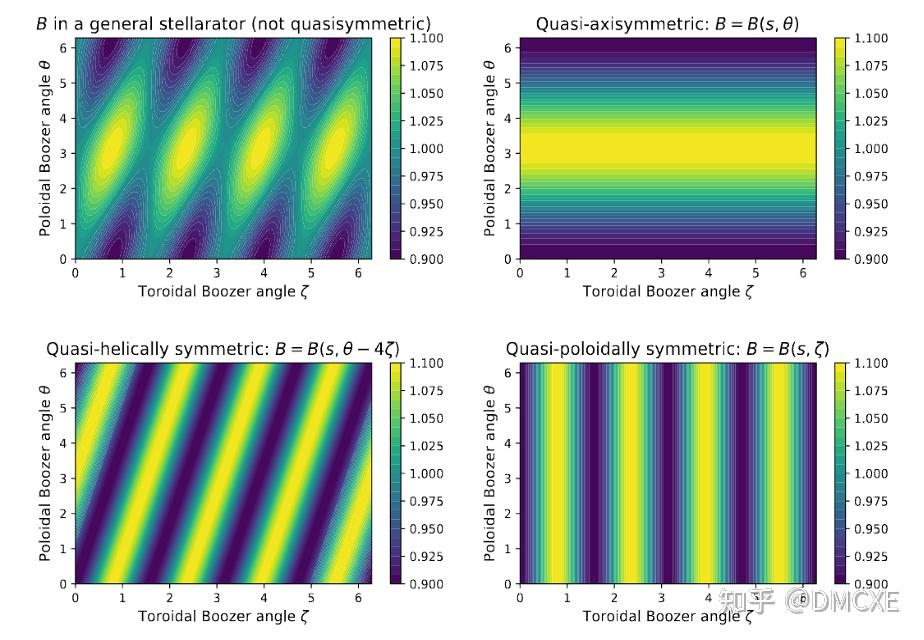
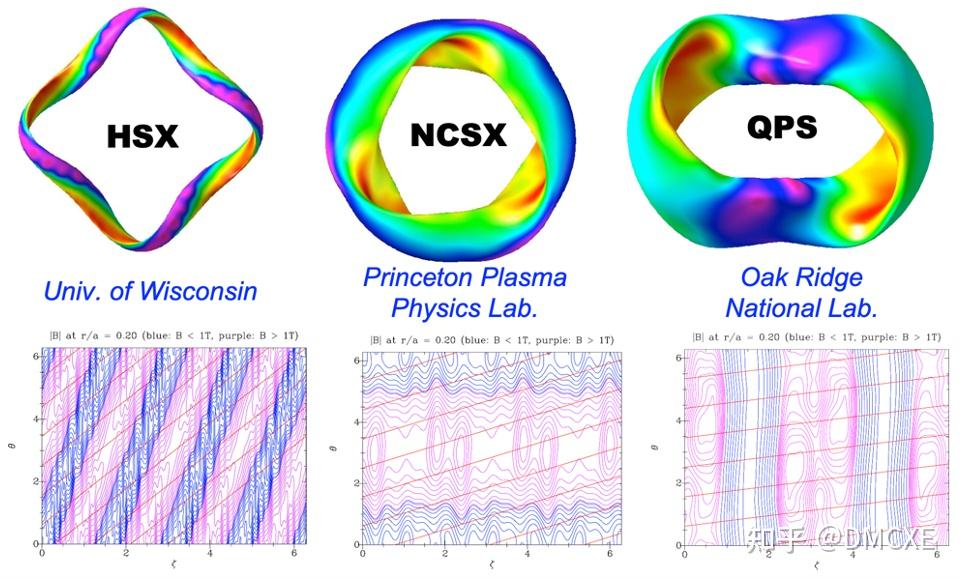
准对称性仿星器概念被提出后，Wisconsin、PPPL、ORNL等多家学术机构开展了位型优化与工程设计，并开展实际装置建造。但最终建成的仅有Wisconsin的准螺旋对称仿星器并验证了准对称性起到了改善约束的作用。而NCSX建造工程则由于复杂的线圈设计在多次预算超支后被停止。

近些年来，随着准对称性理论的完善与数值工具的发展，已经能够健壮的生成高精度准对称位型，其数值上的粒子约束性能已经超过ITER。

Landreman-Paul QA & QH

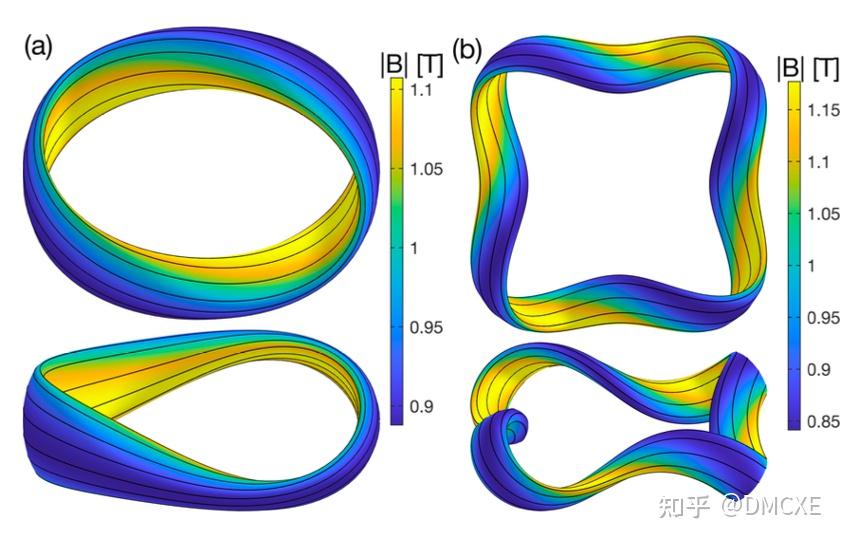
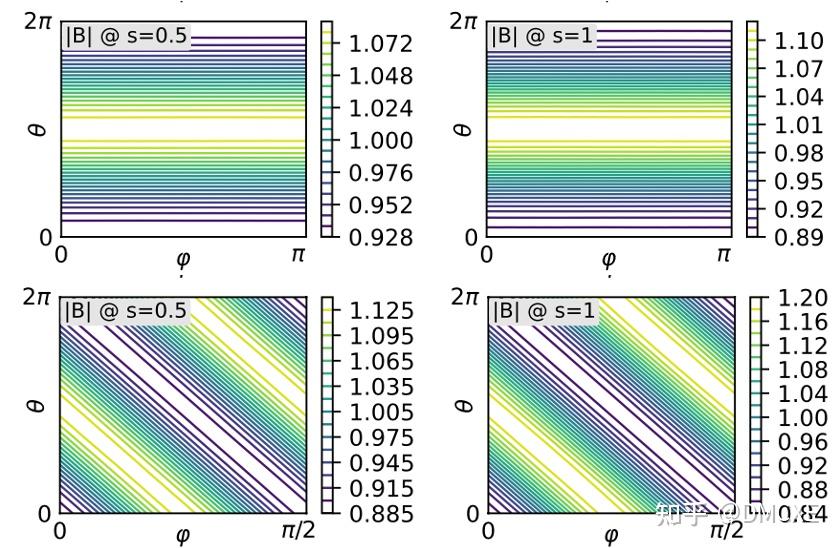
CFQS是中国首台准轴对称仿星器的最外层磁面性质以及磁场强度在Boozer坐标中的分布为：

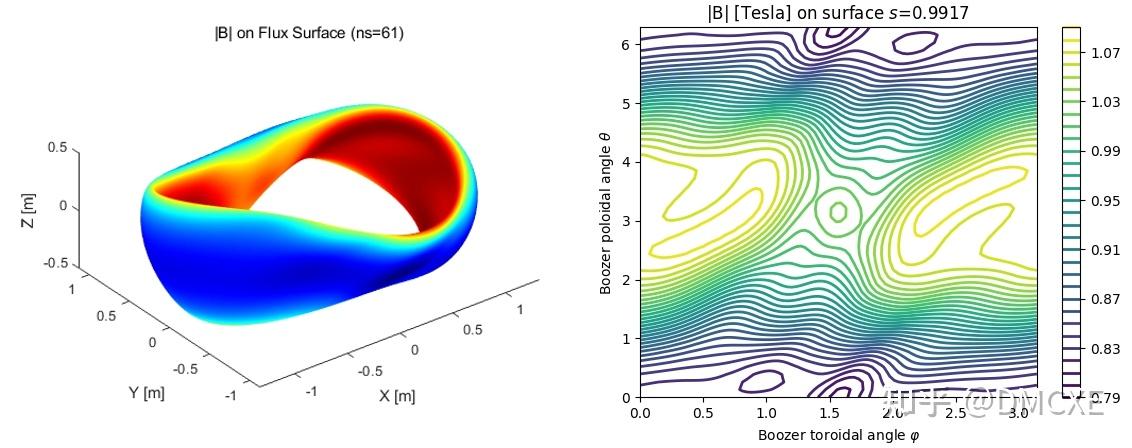
CFQS差一点就成为世界首台准对称仿星器。世界首台准对称仿星器是谁？是一台非常有意思的仿星器——来自PPPL的永磁体仿星器MUSE。产生仿星器的磁场需要复杂的三维线圈，如下所示：

左上：NCSX线圈方案之一；右上：CFQS；左下：HSX；右下：QPS

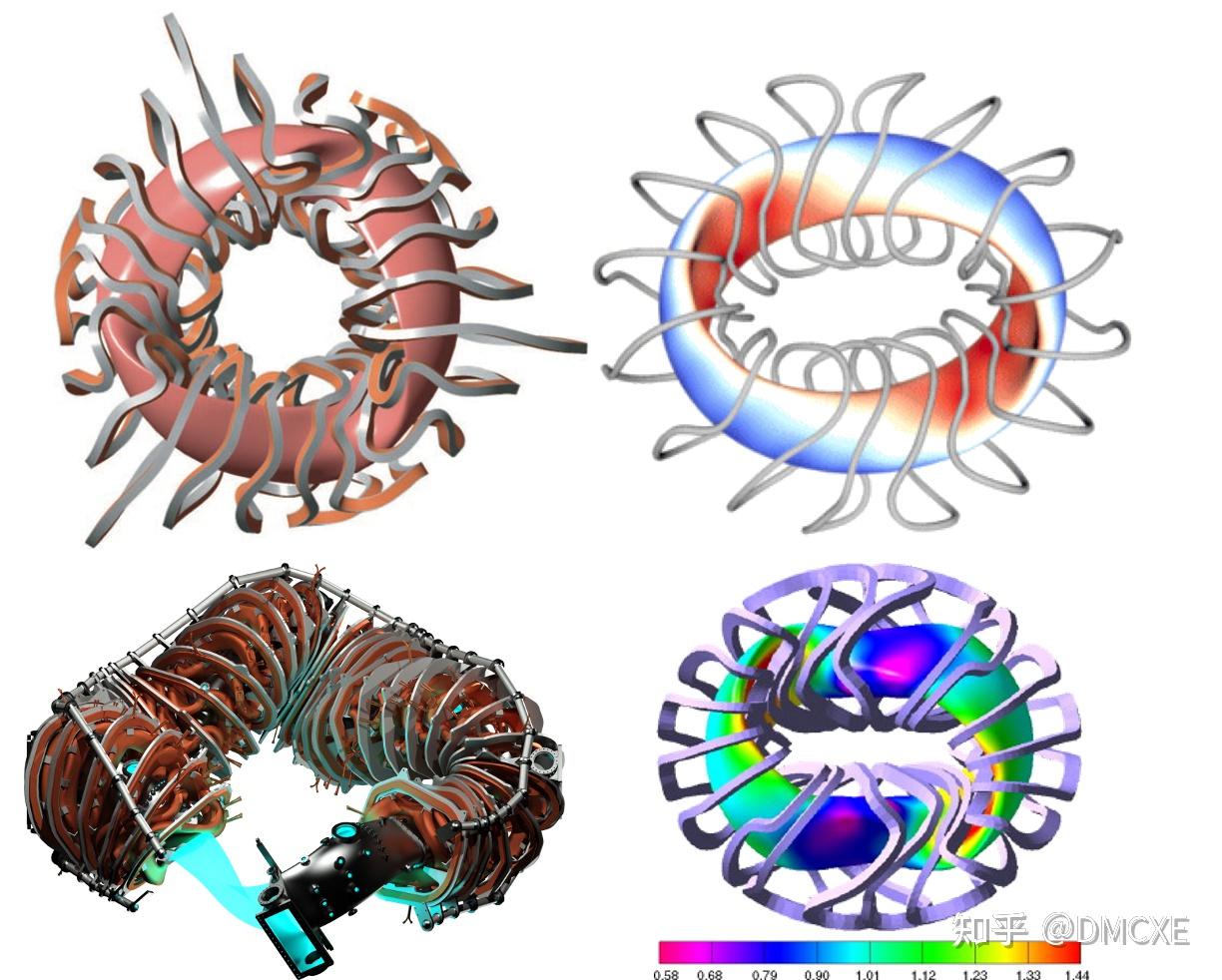
对磁场的塑性可以从另一个角度看待，即把线圈看作电流势与电流密度分布，将其离散化后即可以通过无数个小dipole近似，即永磁体。MUSE是世界首台永磁体仿星器，也是世界首台准对称仿星器

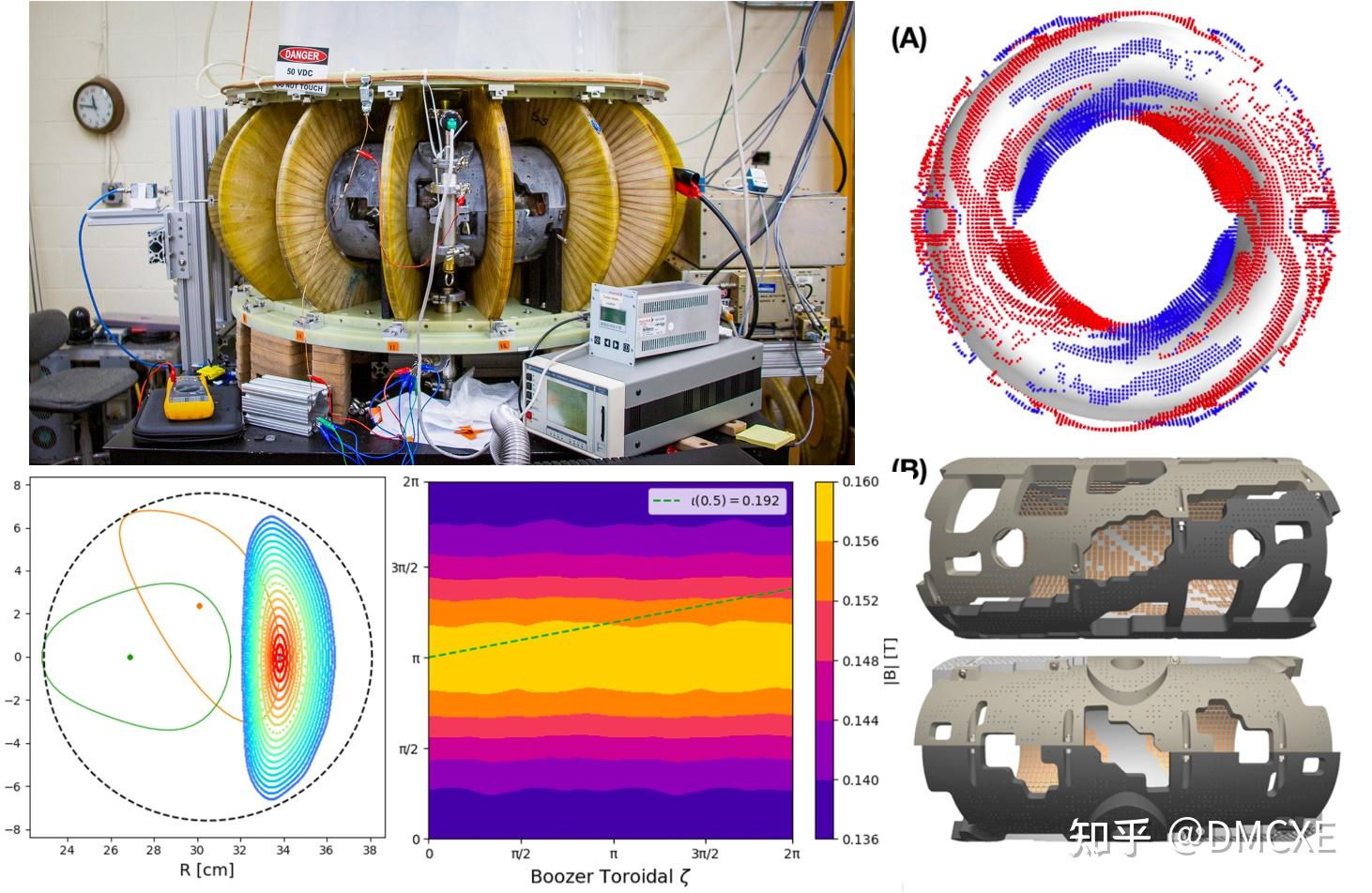
3 趋势

准对称性在无电流下实现了理论上无损失的粒子约束效果。在tokamak中，如果持久的驱动电流是一个困难点，即使存在很多利用自举电流驱动的先进运行模式。这带来很高功率损耗，即聚变堆产生的大部分能量要使得装置本身运行，越高的功率往往需要的驱动功率也越高。聚变电站的最终目标是稳定，最好和裂变堆一样只需要控制临界状态。准对称仿星器，尤其是极向模式数高的那些（QP/QH），往往还能够消除自举电流、降低PS电流，使得真正的稳态运行，这似乎是具备盈利能力电厂所必须的。站在我幼稚的视角看，首先实现的是tokamak，再降低运营成本的路上与其它概念彼此融合。

没有引用，几乎都是可以搜到的。这里还有一个重量级全球最大在运行仿星器W7X没说，它的概念与QP接近但是更高一级，已经通过op1.1的实验验证消除自举电流、降低PS电流、降低新经典输运、几乎稳态等良好的理论特性。

上一篇：怎样使自己处于高能量状态？

下一篇：什么是顶级思维？？

END