如何用一文搞懂什么是快速排序?
快速排序(QuickSort)是一种基于分治法的排序算法。它选择一个元素作为基准,并将数组围绕这个基准(pivot)进行分区(partitions),把基准放在排序数组中正确的位置。
目录
- 快速排序算法如何工作?
- 带有示例的分区算法工作原理
- 快速排序算法示例
- 快速排序的复杂性分析
- 快速排序的优点
- 快速排序的缺点
- 快速排序的应用
快速排序算法如何工作?
快速排序基于分治法,将问题分解成更小的子问题。
算法主要分为三个步骤:
- 选择基准:从数组中选择一个元素作为基准。选择基准的方法不同(如第一个元素、最后一个元素、随机元素或中位数)。
- 分区数组:围绕基准重新排列数组。分区后,所有小于基准的元素位于其左侧,所有大于基准的元素位于其右侧。此时,基准位于正确位置,并获得其索引。
- 递归调用:对基准左右的子数组递归执行相同操作。
- 基本情况:当子数组中只有一个元素时,递归停止,因为单个元素已经有序。
There are mainly three steps in the algorithm:
Choose a Pivot: Select an element from the array as the pivot. The choice of pivot can vary (e.g., first element, last element, random element, or median).
Partition the Array: Rearrange the array around the pivot. After partitioning, all elements smaller than the pivot will be on its left, and all elements greater than the pivot will be on its right. The pivot is then in its correct position, and we obtain the index of the pivot.
Recursively Call: Recursively apply the same process to the two partitioned sub-arrays (left and right of the pivot).
Base Case: The recursion stops when there is only one element left in the sub-array, as a single element is already sorted.
这是快速排序算法的基本概述。
基准选择
选择基准有多种方法:
- 总是选择第一个或最后一个元素作为基准。这种实现方式会在数组已排序时遇到最坏情况。
- 随机选择基准。这种方法更优,因为最坏情况出现的概率较小。
- 选择中位数元素作为基准。尽管时间复杂度理想,但平均效果不佳,因为寻找中位数有较高的常数时间。
分区算法
快速排序的关键步骤是 partition()。有三种常见的分区算法,时间复杂度均为 O(n):
- 简单分区:创建数组副本,先放置较小元素,再放置较大元素,最后将副本复制回原数组。需要 O(n) 额外空间。
- Lomuto 分区:跟踪较小元素索引并交换位置,因其简单性常被使用。
- Hoare 分区:最优的分区方式,遍历数组两侧并交换未分区的元素。
分区算法工作原理(示例)
逻辑简单,从最左侧元素开始,跟踪较小(或相等)元素的索引。如果发现较小元素,交换当前位置元素和 arr[i]。否则忽略。
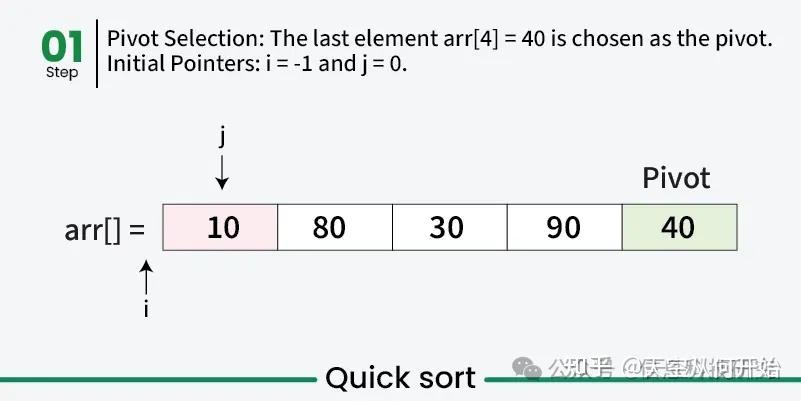
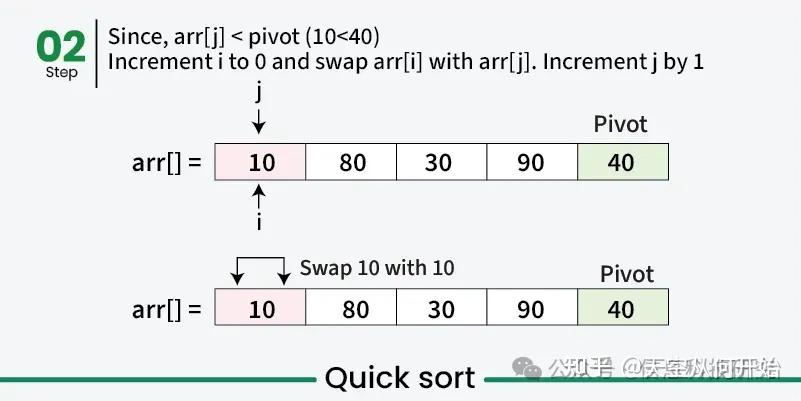
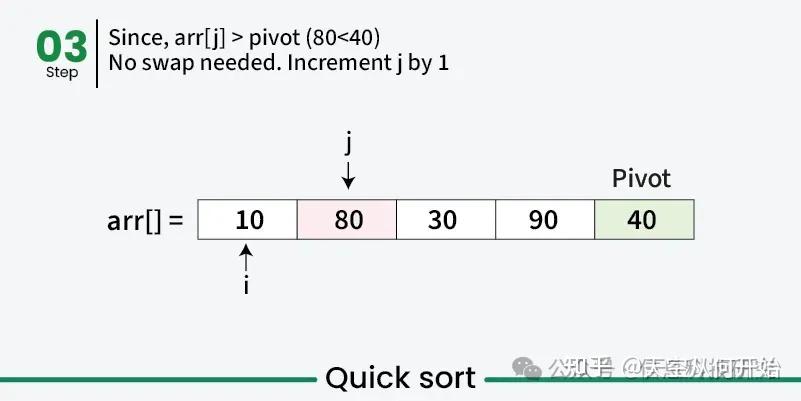
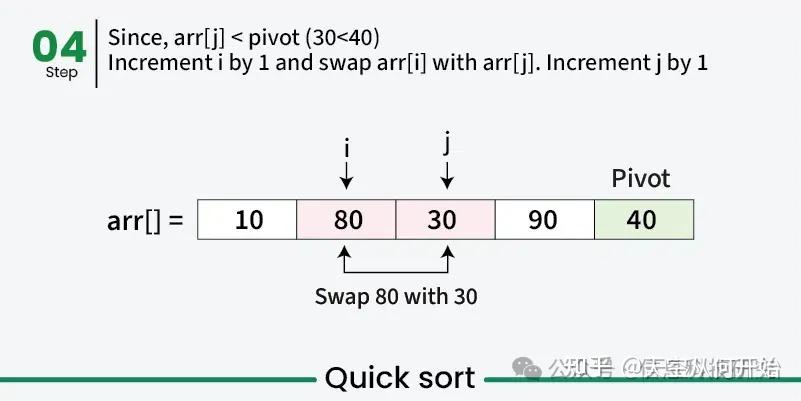
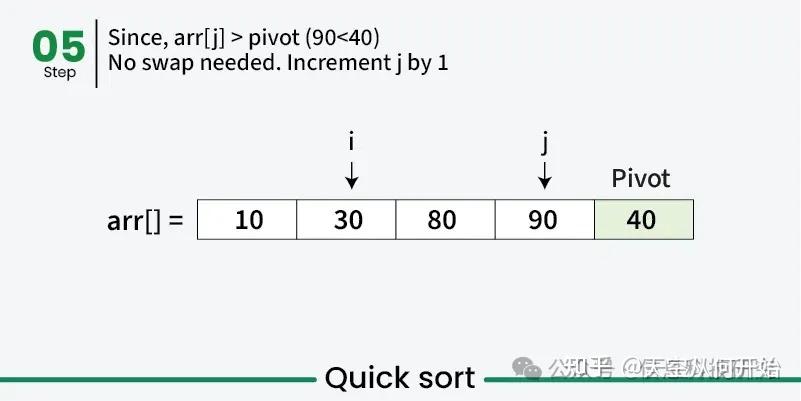

快速排序算法示例
在前面步骤中,我们已经展示了分区过程如何基于基准重新排列数组。接下来,递归应用相同的方法对基准左、右的子数组进行排序,选取新基准并重新分区,直到每个元素都排到正确位置,整个数组有序。
快速排序函数实现
#include <stdio.h>
void swap(int* a, int* b);
// 分区函数
int partition(int arr[], int low, int high) {
// 选择基准
int pivot = arr[high];
// 较小元素的索引,指示当前找到的基准应放置的正确位置
int i = low - 1;
// 遍历 arr[low..high] 并将所有较小的元素移到左侧
// 每次迭代后,low 到 i 的元素都是较小的元素
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(&arr[i], &arr[j]);
}
}
输出
排序后的数组:
1 5 7 8 9 10
快速排序复杂性分析
- 最佳情况:Ω(n log n),当基准将数组分成两个相等部分时。
- 平均情况:θ(n log n),一般情况下基准将数组分成不等的两部分。
- 最坏情况:O(n²),当选择最小或最大元素作为基准(如已排序数组)。
- 辅助空间:O(n),由于递归调用堆栈。
快速排序的优点
- 分治算法,使问题求解更简单。
- 适合处理大数据集。
- 内存开销小,仅需少量额外内存。
- 对缓存友好,因在同一数组中排序。
- 对于不要求稳定性的情况下,是最快的通用排序算法。
- 支持尾递归,可优化递归调用。
快速排序的缺点
- 最坏时间复杂度为 O(n²),当选择基准不理想时。
- 不适合小数据集排序。
- 不是稳定排序,无法保留相同键值元素的相对顺序。
快速排序的应用
- 适合大数据集排序,平均时间复杂度 O(nlogn)。
- 用于分区问题,如寻找第 k 小的元素或用基准划分数组。
- 随机算法中,表现优于确定性方法。
- 在加密中用于生成随机排列和不可预测的加密密钥。
- 分区步骤可并行化,提高多核或分布式系统的性能。
- 理论计算机科学中,用于分析平均复杂度和开发新技术。
参考链接:
https://www.geeksforgeeks.org/quick-sort-algorithm/