一杯100 度的水可以把一杯0 度的水最多加热到多少度？63.21度是极限了吗？

这是一个非常棒的热力学问题。事实上，答案可能会令你震惊：我们可以经过一系列操作，最终把100℃的水降到0℃，而把0℃的水升温到100℃。

理论依据：用熵叙事

我们知道，对于孤立体系，讨论一个热力学过程能不能发生的根本判据是熵不能减少，也就是：

其中S代表体系的总熵。而对于 的过程，我们称之为可逆过程。当然，我们额外还有能量守恒的约束： ，U代表体系的总能量。

因此，对于题设中的孤立系统：A杯装有0℃的水，B杯装有等量100℃的水，假设我们用一些复杂的热力学装置将它们连接起来，然后考虑如下过程：

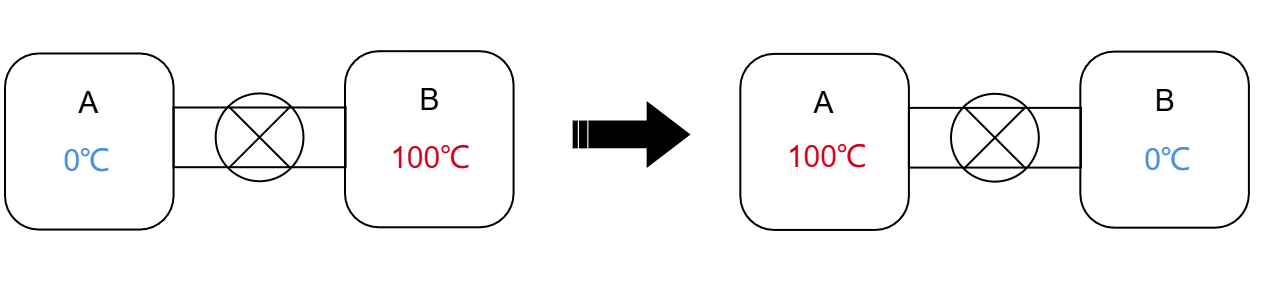
在这一过程中，如果内部装置的初始状态和终末状态完全相同，而我们知道A、B两杯水的热力学性质也完全相同，因此整个过程的初态和末态的熵也应该完全相同。 ，这样的过程在热力学上是允许的。

那为什么我们日常生活中，从来不会发生过这种反常的传热呢？答案也隐藏在熵中：如果我们直接把低温物体A和高温物体B接触，考虑A给B传递热量 （先假设这是一份很少的热量，因此忽略A和B的温度变化），则总的熵变为：

由于 ，因此当且仅当 时 。换句话说，只有A从B吸热的过程是热力学上允许的。因此直接接触会导致B不断传热给A，直到二者温度相同，整个过程的热量和熵变就是上述 和 的积分。可以得知这一过程 ，熵增加了，是不可逆的。换句话说，此时如果我们想回到初始 的状态，或者达到A与B温度互换的状态，都是不可行的了——因为我们需要再构造 的步骤来让两步总的熵变等于0。

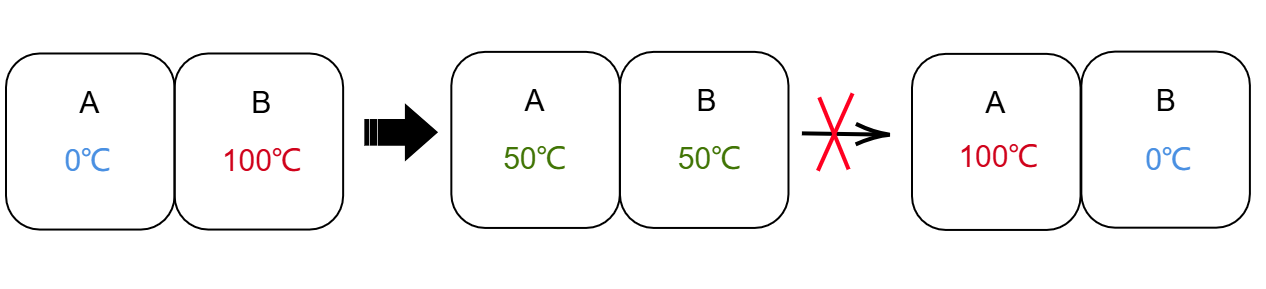
这也给了我们新的启发：想要达到温度互换的效果，必须要足够小心——要保持每一步操作都是 的可逆过程。

因此，仅靠传热是行不通的。因为两个物体间传热，能量守恒 要求：一个物体放出多少热量，另一个物体就要吸收多少热量。只要A、B温度不相等，上一个公式就揭示了这一步必然会导致熵增加。

为了破解这一局面，我们必须引入更灵活的热力学系统，来把能量以非热量的形式交换。例如理想气体，我们可以利用体积功：

还有电磁系统，我们可以利用电功、磁矩和磁场交互的功等等。事实上，一个“夹杂了做功私货的可逆传热”就是大名鼎鼎的卡诺热机。

物理构造：卡诺热机

卡诺热机干的事情就是：高温热源吸热，低温热源放热，热量差以做功的形式放出。整个过程完全可逆地进行，即 。能量交换关系如下：

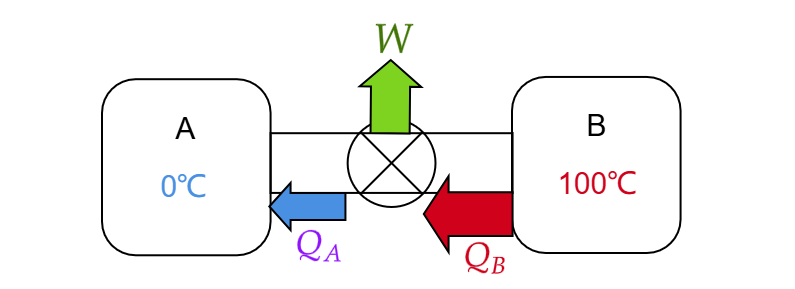
实现这一过程的热力学装置很多，例如我们上节提到的理想气体就可以构造卡诺循环：

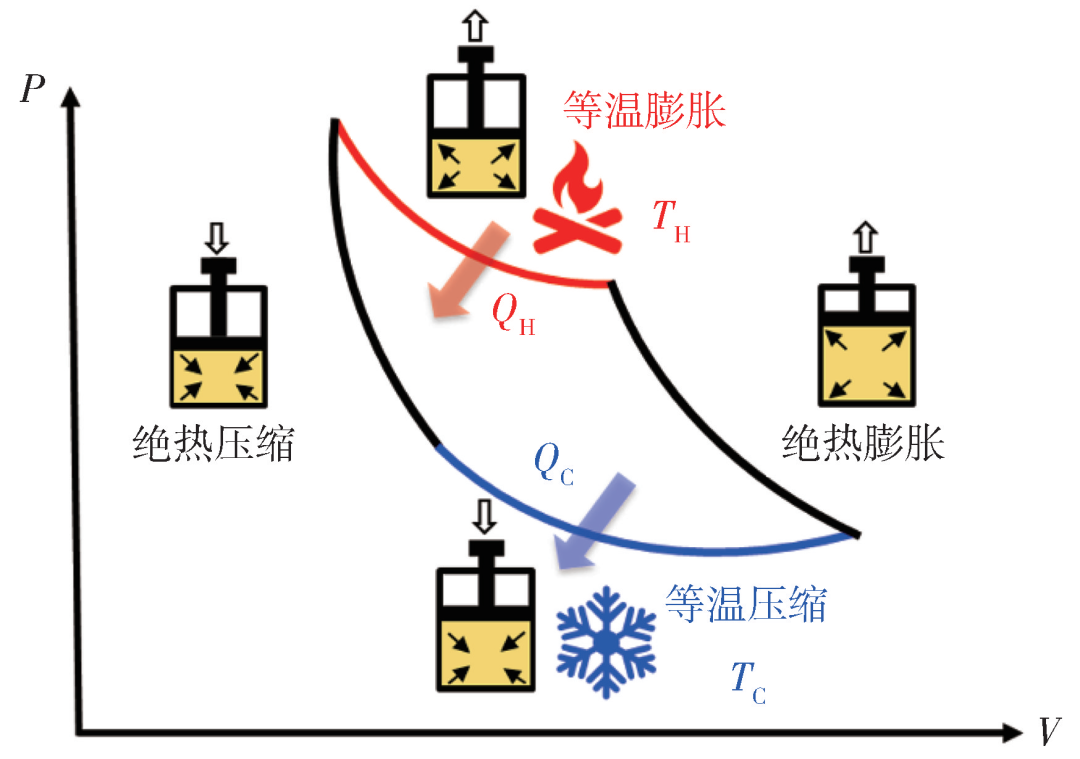
循环一次的过程完美符合前述对卡诺热机的描述。还要注意：卡诺循环运行始末，热机的内部状态是复原的。这保证了整个过程不只是熵意义下的可逆，还是操作意义下的可逆：卡诺热机是可以倒着开的，你可以输入功以从低温热源吸热，并放热给高温热源。

相信聪明的读者已经get到怎么实现本文开头提出的目标了：

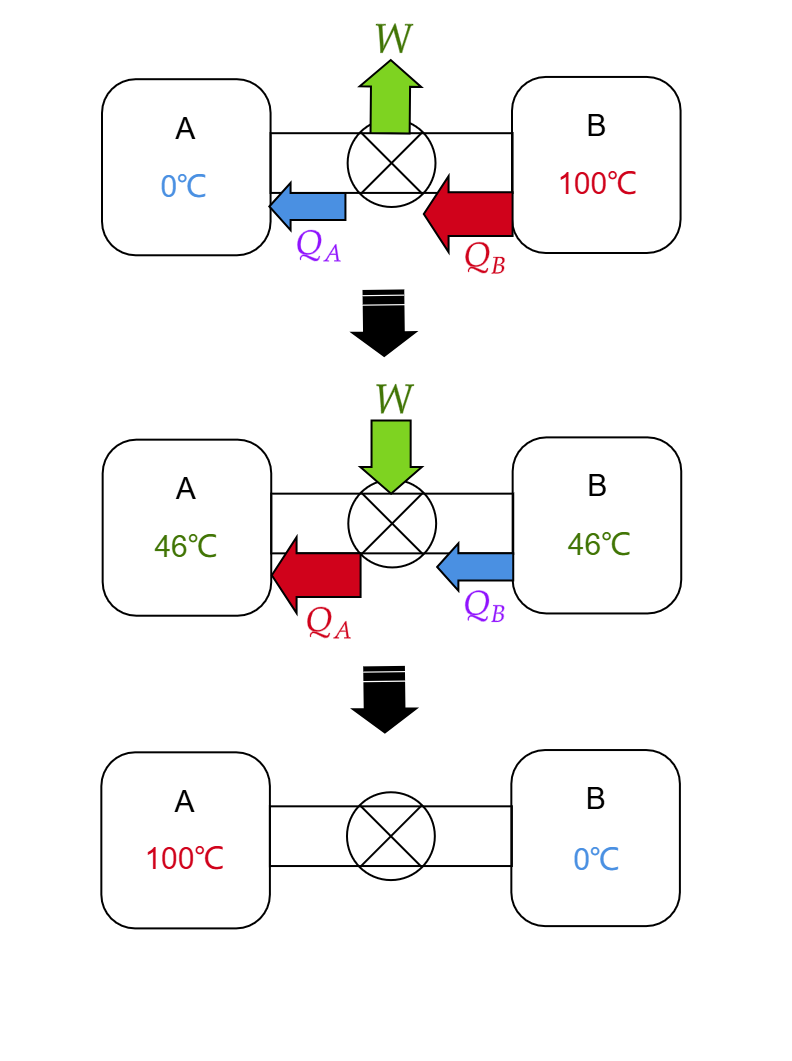
先用卡诺热机把A与B的温度拉平，然后再倒开卡诺热机（此时A和B扮演的角色互换），用刚才产出的功把热量泵到A中去。

当然其中涉及到一个存储功的问题，可以用可逆电池之类的东西来实现，或者用一些力学装置。总之，整个过程在理论上是完全可行的。我们从0℃的A和100℃的B出发，利用卡诺热机，得到了100℃的A和0℃的B，且热机装置的始末状态完全相同。