为什么 lnx 求导是 1/x?
其实,我想对题主说,你提的问题一点都不弱智。恰恰相反,这是个非常有意义的问题。我们学习一门知识,尤其是数学知识,要知其然,更要知其所以然。今天,我尝试从“如何去定义“的角度出发来解释这个问题,不玩公式推导的符号游戏。希望能带来新的启发。
为解决对数函数的问题,在未给出定义以前,我们应该先研究指数函数。最开始,我们有指数的基本性质:
根据基本性质,你应该能够推导出一些指数函数的运算法则,例如:
上述公式中的 ,,使得指数函数在实数域上也有了定义。 (经@朱俊辉 指正)
我们先研究指数函数 的一阶导,根据极限:
注意框起来的部分,一个关于 的函数,我们姑且叫它“谜之函数”
,一个迷一样的函数。
我们对 所知甚少,但至少应该了解它的几何含义: 指数函数
在
点处的斜率。
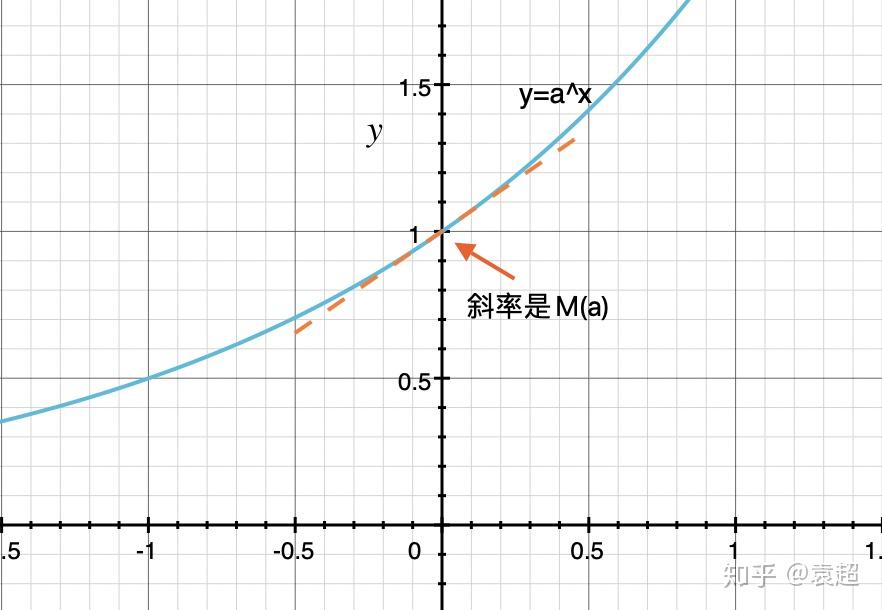
为了搞清楚 究竟是什么,我们假设有一个“迷之数”
, 使得
。虽然,我们不清楚
究竟是什么,但有了这样的假设,非常自然的:
那么,数 一定就存在的吗?不妨来验证一下,考虑
,
。
将 带入到
:
,
。
对比我们上面的假设可以发现,数 确实是存在的,只需令
,此时的
即为
。
我们绕了一大圈,还没搞清楚 ,又引入了数
,这么做究竟是为什么呢?回顾一下,考虑一个指数函数是非常自然的,更进一步,定义在实数域上的指数函数也很显然。我们在计算指数函数的导数过程中,遇到了“棘手”的
,但是,通过引入假设的数
,似乎又没那么难了。而且我们证明了,数
是一定存在的。
有了指数函数,定义其反函数称为对数函数。你应该记得什么是反函数,几何意义是将函数图像以轴 对称,计作
。以数
为底的指数函数具有良好性质,其反函数是以数
为底的对数函数,记作:
。
一个问题:已知 是
的反函数,那么
答案: 。令
,
,取
的反函数
。因为
是
的反函数,所以,当
,
,推出
。可以这样想,反函数是关于
对称,那么反函数的反函数则就是其本身了。
最后,我们解决 ,令
:
根据隐函数微分法:
整理可得:
证毕。
最后,聪明的小伙伴可能已经发现了,那个“迷之函数” 其实就等于
。相关证明留作课后习题,请读者自行完成。