 "最大值"搜索结果 1 条
"最大值"搜索结果 1 条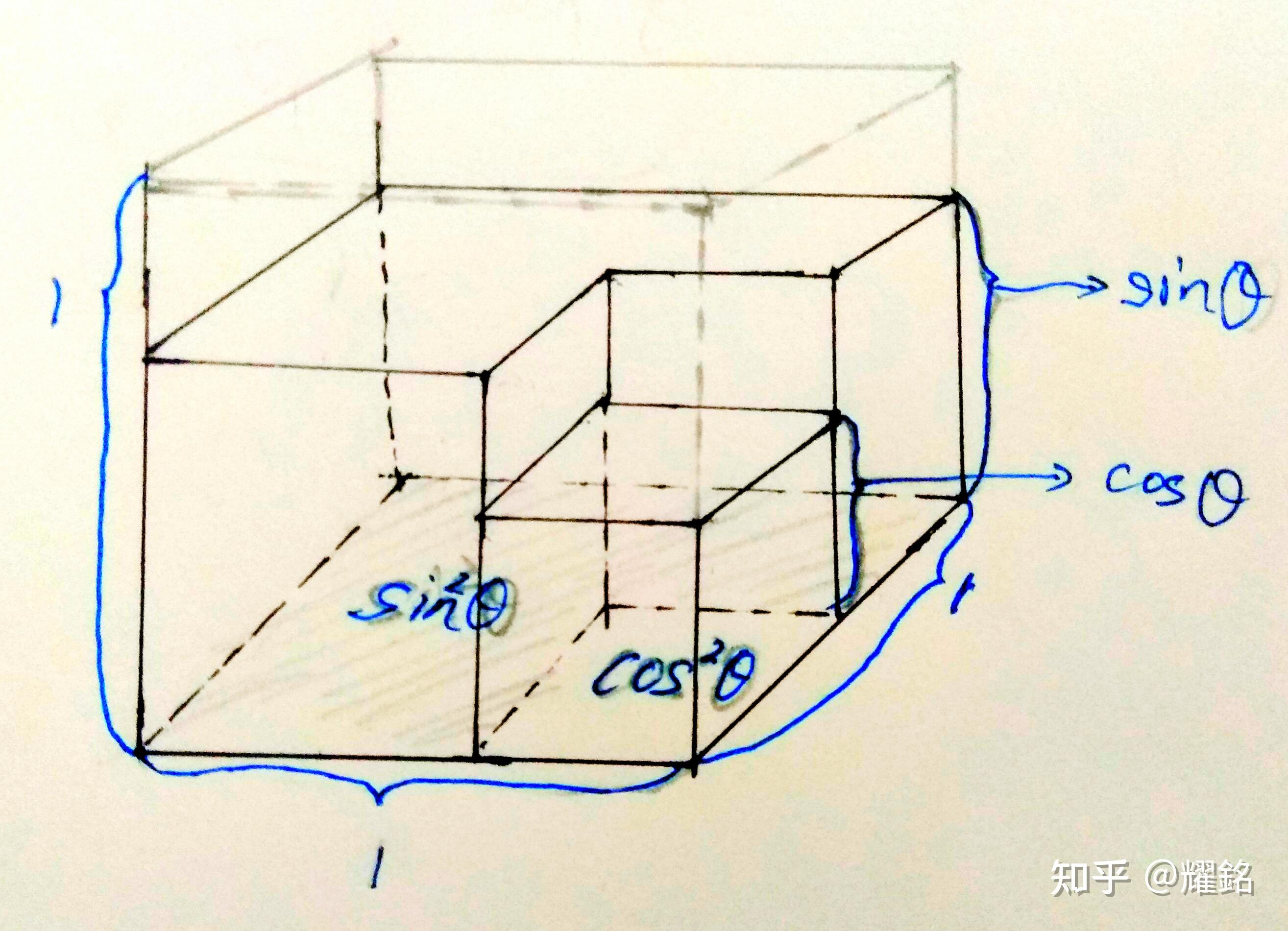
如何不求导求 cos³x+sin³x 的最大值?
如果大家有被大佬离谱的代数变形虐到,就拿纯几何无字证明洗洗眼叭~ 稍唠叨一下,(其实光看图就行) 首先最大值对应的cosθ和sinθ一定非负,比起负体积当然不如其所对应的正体积大嘛 然后,在边长为1的正方体底面,任取一块面积为cos方θ,并做这块面积对应的高cosθ;剩下的面积就一定是sin方θ,并作高sinθ(为了图好看我取了个矩形为cos方θ) 这两个体积固然恒小于等于外面的正方体 (不论是瞪眼法,还是照着图移动两个体…