如果一个方向突然出现很多培训班,那说明了什么?
先说结论:
1、教培行业不会永远扩张下去的,这是我自初中开始就秉承的理念。
2、某个方向的培训行业突然扩张,实际上在增加这个行业发展的负担。
3、培训行业的突然扩张,说明做培训开始比做这个行业本身更赚钱了。剩下的就各人自己考虑吧。
我们假设A行业的利润作为基础的参数。
A行业的教培成本,就是该行业的教培行业的行业利润,我们把a行业的教培行业标记为b行业。
我们先设定,有着如下的关系:
- 行业利润除以从业人数的商减去教培成本,等于成员待遇。
- 从业人数小于潜在从业人数,
- 从业人数除以潜在从业人数,等于就业压力
- 教培成本正比于就业压力,
- 潜在在从业人数反比于教培成本,
- 行业利润正比于从业人数,
- 成员待遇正比于潜在从业人数
- 行业利润的增长慢于从业人员的增长
- A行业的教培成本就是该行业的教培行业的行业利润,我们把a行业的交配行业标记为b行业,
- 上述所有规则同样适用于b行业与a行业
上述规则,很多或许还有可供商榷的空间。而且很多关系不可能是简单的线性关系,而是更复杂的什么东西。但我们先一切从简来试试(毕竟复杂的我也不会)。
现在假设a行业的行业利润是一个以线性单增的函数为基础,同时受到其他的以上述关系影响的东西。
现在在尝试,去简单的模拟它们之间的数量关系,得到这样的表现:
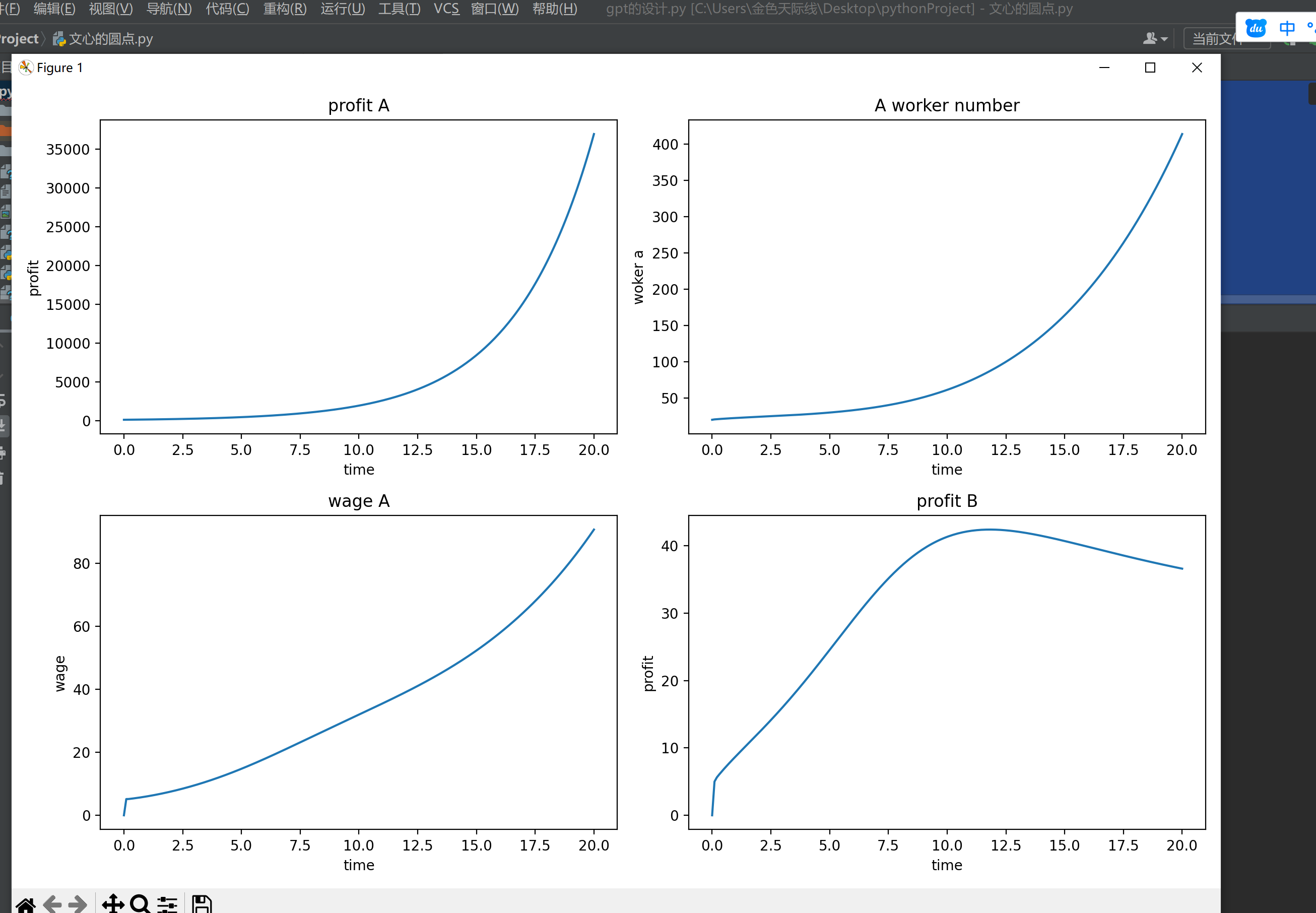
在行业a的利润不断增加的同时,该行业的从业者的数量也在增加,工资也在增加。
但是培训a行业的培训行业b的利润,在先上升到峰值,后略微下降。如果把时间线拉长,那么培训行业的利润就会稳定在某个区间。
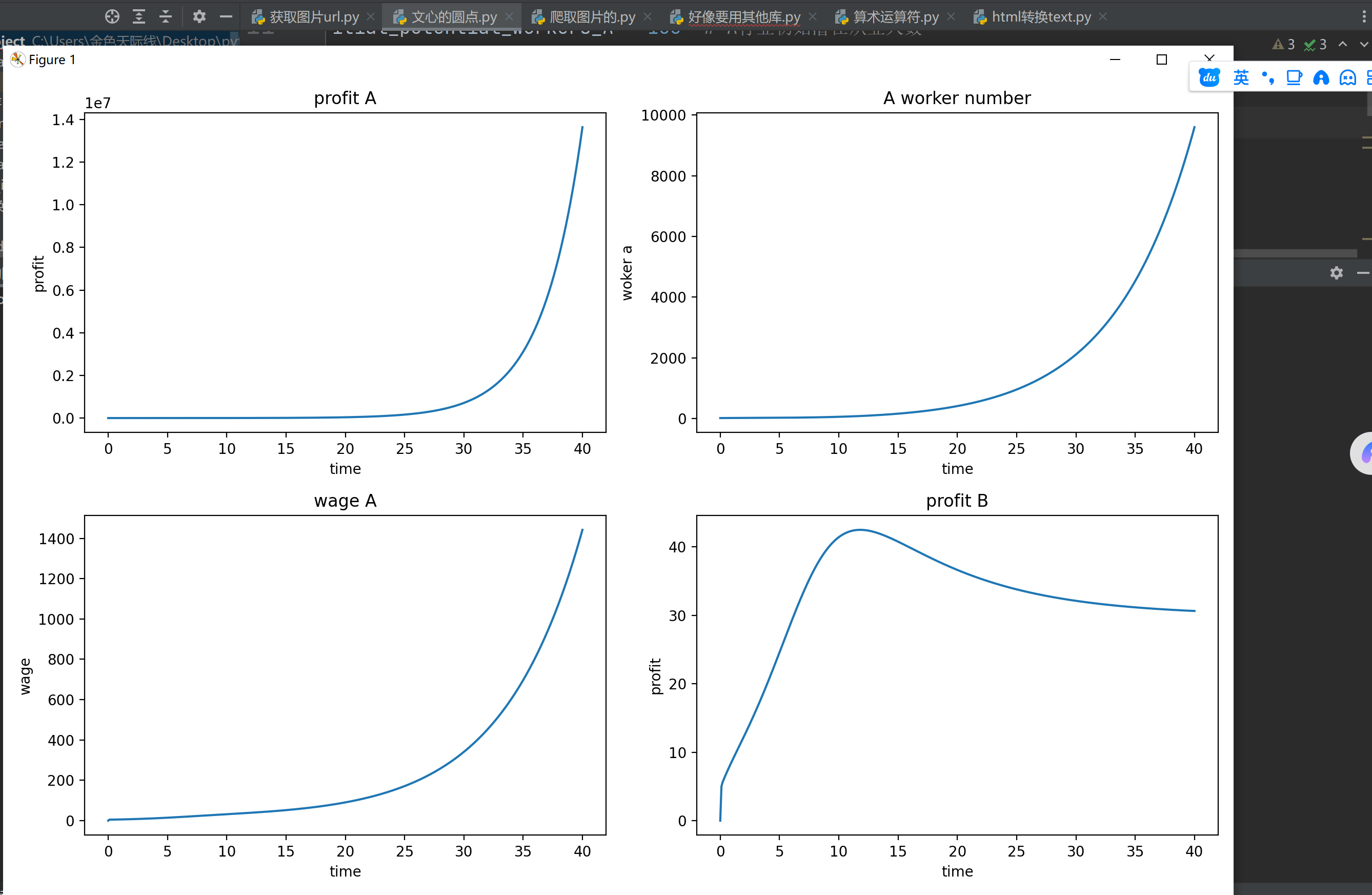
教培行业不会永远扩张下去的。这也是我自初中开始就秉承的理念。
如果这个行业的收入只是线性增长的话,那么教培行业的扩张,会强烈的打击这个行业的发展(但我估计这应该是我参数没有设置正确的问题,毕竟曲线的变形程度太大了)
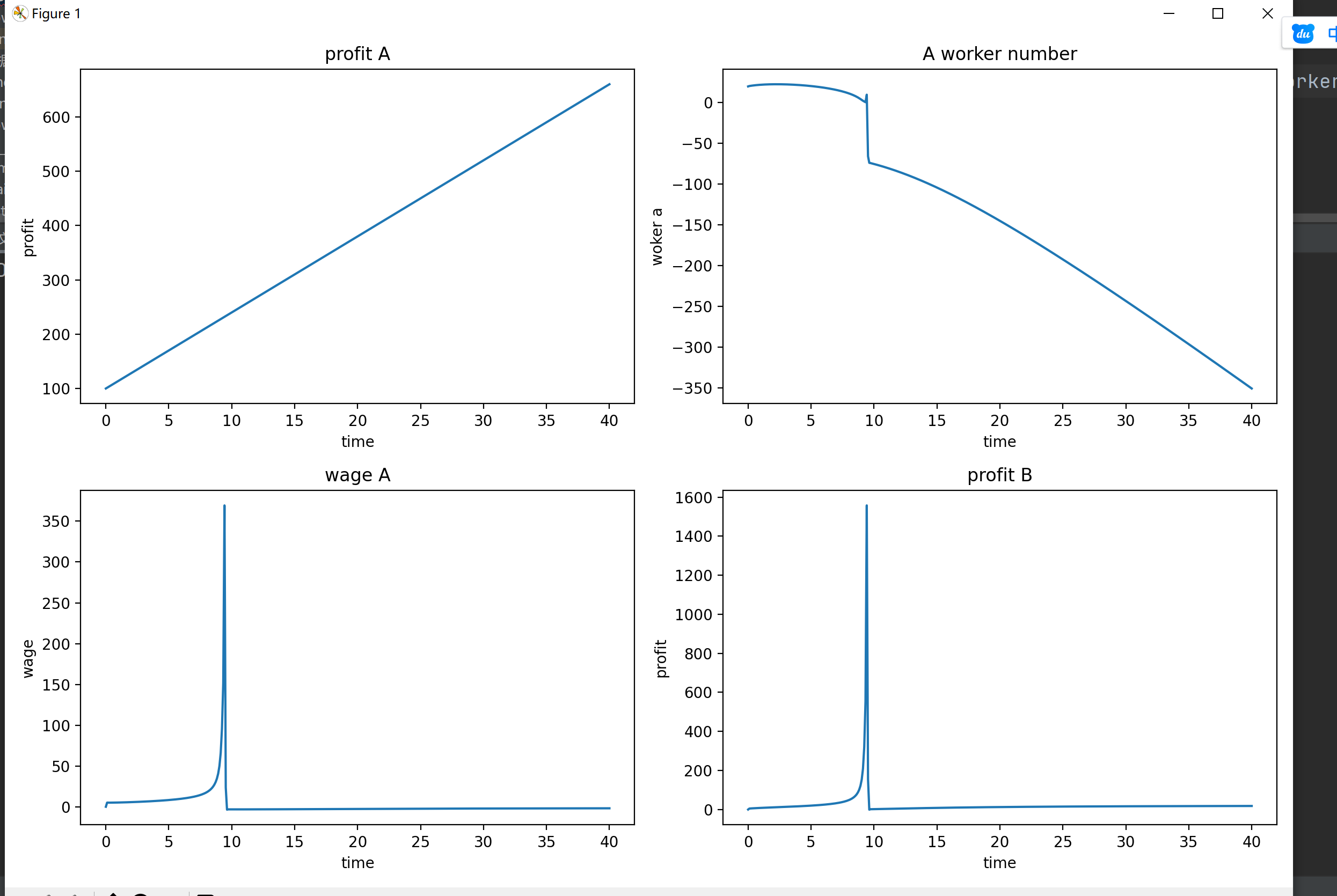
所用代码如下(后续应该会尝试将其调整得更加复杂):
import numpy as np
import matplotlib.pyplot as plt
# 初始化参数
k1, k2, k3, k4, k5 = 1.0, 0.5, 2.0, 0.3, 0.1
r = 0.3 # A行业利润的自然增长率
rw = 0.2 # A行业利润随从业人数增加而造成的增长
initial_profit_A = 100 # A行业初始利润
initial_workers_A = 20 # A行业初始从业人数
initial_potential_workers_A = 100 # A行业初始潜在从业人数
# 时间设置
t = np.linspace(0, 20, 200) # 从0到20年
# 初始化数组来存储变量
profit_A = np.zeros(len(t))
workers_A = np.zeros(len(t))
potential_workers_A = np.zeros(len(t))
wage_A = np.zeros(len(t))
training_cost_A = np.zeros(len(t))
profit_B = np.zeros(len(t)) # B行业利润
# 初始条件
profit_A[0] = initial_profit_A
workers_A[0] = initial_workers_A
potential_workers_A[0] = initial_potential_workers_A
# 尝试模拟运行
for i in range(1, len(t)):
# A行业利润增长
profit_A[i] = profit_A[i - 1] + r * profit_A[i - 1] * (t[i] - t[i - 1]) + rw * workers_A[i]
# A行业的从业待遇
wage_A[i] = profit_A[i]/workers_A[i-1]
# A行业从业人数增长
workers_A[i] = workers_A[i-1] + k5 *(wage_A[i]-0.5*training_cost_A[i-1])
# A行业潜在从业人数(假设为常数或根据实际情况调整)
potential_workers_A[i] = potential_workers_A[i-1] + (3*wage_A[i]-training_cost_A[i-1])
# A行业教培成本
training_cost_A[i] = k1 * (potential_workers_A[i-1] / workers_A[i-1] )
# B行业利润(等于A行业的教培成本)
profit_B[i] = training_cost_A[i]
# 绘制图像
plt.p(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(t, profit_A, label='profit A')
plt.title('profit A')
plt.xlabel('time')
plt.ylabel('profit')
plt.subplot(2, 2, 2)
plt.plot(t, workers_A, label='A worker number')
plt.title('A worker number')
plt.xlabel('time')
plt.ylabel('woker a')
'''
plt.subplot(2, 2, 2)
plt.plot(t, potential_workers_A, label='potential_workers_A number')
plt.title('potential_workers_A')
plt.xlabel('time')
plt.ylabel('potential_workers_A')
'''
plt.subplot(2, 2, 3)
plt.plot(t, wage_A, label='wage A')
plt.title('wage A')
plt.xlabel('time')
plt.ylabel('wage')
plt.subplot(2, 2, 4)
plt.plot(t, profit_B, label='profit B')
plt.title('profit B')
plt.xlabel('time')
plt.ylabel('profit')
plt.tight_layout()
plt.show()
。