为什么部分大一学生认为线性代数听不懂？

发布时间：

2024-10-04 02:10

阅读量：

线性代数听不懂？初中的二元一次方程组会不会解？

我们知道方程 ax =b 很简单，只需要一步就能解出来，x = b/a。

比如「我买了4个包子，花了6块钱，每个包子多少钱」就可以通过解「4x = 6」得到「x = 1.5」

这里列方程的关系是「个数a」乘以「单价x」等于「总价格b」

那如果问题改成「我今天买了4个包子，2个馒头，花了7块钱，昨天买了2个包子，4个馒头，花了5块钱」，列出来的就是方程组①，

$4x_1 +2x_2 = 7$

$2x_1+4x_2=5$

这时候未知数是包子和馒头的单价，分别叫做x1和x2，第一天买的个数分别是a11、a12，总价格b1，第二天个数是a21、a22，总价格b2。

$a_{11} x_1+a_{12} x_2=b_1$

$a_{21} x_1+a_{22} x_2=b_2$

这时候方程的个数虽然变多了，但其实本质上还是「个数A」乘以「单价x」等于「总价格b」

这里A有4个元素，x有2个元素，b有2个元素，都是矩阵

$A=\begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{21} \end{bmatrix}$

$x=\begin{pmatrix} x_{1}\\ x_{2} \end{pmatrix}$

$b=\begin{pmatrix} b_{1}\\ b_{2} \end{pmatrix}$

这里行列数一样的叫做方阵，N行一列的就是向量（列矩阵），通过矩阵乘法规则组成上边的方程组。

$\bold A x = b$

那么这个方程要有确定的解的话，2个未知数至少有2个方程才行，所以A最起码得是个方阵。

只是方阵还不够，比如下边这个方程组②是没法解的：

$4x_1 +2x_2 = 7$

$8x_1 +4x_2 = 14$

因为这两个本质上是一个方程，第二个是第一个的二倍，这就是第二个方程表达的关系跟第一个是一样的，并没有新的关系，这两个方程是相关的，不是独立的。

如果我们按照解方程的常规思路进行消元，将第二个方程两边除以2，再跟第一个方程相减，这就叫做矩阵的行变换。

行变换以后，将方程进行化简，发现独立的方程只有一个，没法求解两个未知数，这里独立方程的个数就叫做系数矩阵的秩，如果秩与行列数不等，叫做不是满秩的，那方程就没法求解。

另一方面，就像求解ax=b需要方程两边除以a，这个矩阵方程 $\bold A x = b$ 需要一个类似的运算，也就是取逆矩阵得到

$x = \bold A^{-1}b$

根据初中二元一次方程组的求解我们就知道

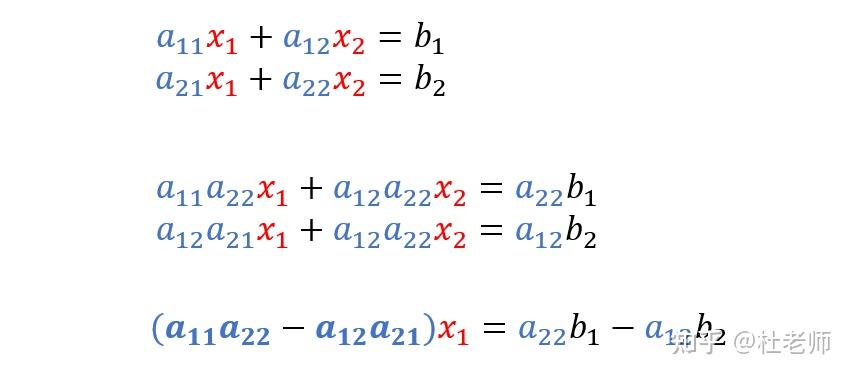
$\displaystyle x_1 = \frac{-a_{12} \cdot b_2 + a_{22} \cdot b_1}{a_{11} \cdot a_{22} - a_{12} \cdot a_{21}}$

$\displaystyle x_2 = \frac{a_{11} \cdot b_2 - a_{21} \cdot b_1}{a_{11} \cdot a_{22} - a_{12} \cdot a_{21}}$

如果分母不等于0，那么这个方程就是有确定解的，而分母等于零，方程就没法求解。

线性代数里，这个分母不等于0，那么A的逆矩阵 $\mathrm A^{-1}$ 就存在，而分母等于零， $\mathrm A^{-1}$ 就不存在。

而分母是由系数矩阵A里的四个元素计算而来的，给它取个专业的名词，这就是系数矩阵的行列式

$|\bold A|=a_{11} \cdot a_{22} - a_{12} \cdot a_{21}$

行列式不为0，方程就可以解，这种系数矩阵就叫做非奇异矩阵。

比如方程组①的系数矩阵行列式 $\begin{vmatrix} 4& 2\\ 2&4 \end{vmatrix} =12$ ，包子馒头的方程就可以解。

行列式等于0，方程没法求解，这种系数矩阵就叫做奇异矩阵。

比如方程组②的系数矩阵行列式 $\begin{vmatrix} 4& 2\\ 8&4 \end{vmatrix} =0$ ，不满秩的方程就没法解。

结合二元一次方程组，简单介绍一下线性代数里的几个基本概念，我想如果这样讲的话，大一的学生听起来不至于那么难懂。

而如果按照很多教材的编写顺序，一上来先讲行列式复杂的算法，然后再讲矩阵复杂的运算，讲了矩阵的秩，后边才讲向量的相关性，然后才出现了线性方程组，那很容易听起来一脸懵。

END