初一没学好,初二数学怎么学?
本文是写给那些很努力,但是数学成绩提不高(中考难度数学140分以下)的孩子和孩子家长的。对于成绩的提高,很遗憾,和绝大多数事情一样,老师只是外因,但最重要的却是内因。
有两种孩子我是不太愿意在他们身上浪费时间的:
1. 懒惰,自己不想学习的孩子。有一句话叫做“天助自助者”,如果一个人自己不愿意改变,没有人能够帮得了他。
2. 自以为是。有些孩子扫一眼别人的中肯建议,然后不加以尝试和实践,便说“这个方法不适合我”。不好意思,你没有那么特别。人的共性远远大于个性,这是教育有存在必要的逻辑基石。我不相信“适合你的方法”,只相信科学的方法。
如果你不属于上面两种人,很好,请继续往下看:

那么很多孩子的数学为什么学不好呢?我分析了以下的原因:
1. 蒙,猜,凭感觉做题的坏习惯 – 数学是一门极为严谨的学科!
如果评选一门学科的严谨性,那么数学绝对是当之无愧的第一,没有之一。数学本身是极为美妙的公理演绎体系(axiom-deduction system),换句话说,只要构建数学各个分支的基石 – 公理是正确的(+定义无矛盾),那么其所有的结论(定理)都必须是正确的。而数学解题也是如此,每一道题目的求解在逻辑上必须是完美的:
(1)对于求证题(判断题),只要已知和定理是正确的,那么被证明的命题一定是正确的;
(2)对于求解题,求出来的解一定是符合题目条件的所有解,既没有增根也不应该失根。
因此我们在数学学习和解题中必须十分重视严谨性这一点,具体就是要做到每一步都要有理有据(我这里不想过多深入,有兴趣的同学可以查一下,数学大多数的推理需要符合假言推理这种演绎推理模式。而求解题要对题目条件进行充要变换才能做到无失根,无增根。)
我经常对学生说: 学数学不能靠感觉,不允许说“我觉得…”,“我以为…”,每一步都要有理有据。这一点其实从初中平面几何开始就十分强调了:
所有初中学生一开始学习平面几何的时候,教材会要求同学们在每一步后面用括号把这一步的理由(利用了什么定理,定义)写下来,例如:

括号里面写出来的“对顶角相等”或者“ASA(角边角定理)”就是这一步的理由。
当同学们对这种理性思维开始习惯了,慢慢的教材也就不再对此进行要求。
然后遗憾的是,很多同学并没有形成这种理性思维,即每一步都有理有据的习惯。他们在解题的时候继续凭感觉,肆意妄为,说得难听些,这样的孩子恐怕连数学的门都还没有入。因此,我的建议是,如果你有乱猜,凭感觉做题的坏习惯:
1) 从今天开始,老老实实地每一步用括号把理由写到后面,哪怕做题慢一些,也要把这个习惯养成;
2) 从今天开始,你的错题只有可能是粗心做错或者概念不清做错,绝对不允许是因为乱猜出错。
等这个习惯开始养成,你看待数学会有第一个质变 – 原来数学是如此严谨的,是如此美的东西。你开始理解难怪数学可以拿到满分,而语文却很难(例如作文的好坏就有一定的主观性)。你也开始意识到理性思维的作用。这对你今后,无论是中学阶段的物理,化学等的学习还是到了大学,研究生阶段对金融,工程等的学习都十分重要。
顺便说一句,我教授的高中生不少也有这个瞎蒙的毛病,如果你是一位高中生或考研的大学生而很遗憾你也有这个烂习惯,也请你下功夫改掉。
那么数学不允许猜测吗?不,事实上数学解决问题中大量使用各种似真推理和猜想。但无论如何猜测,最后的结论必须要能够证明,必须要符合逻辑。大胆猜想,小心求证!这里我们强调的就是“小心求证”这4个字。
2. 基础不扎实,不会用数学语言来学习概念,定理



尽管初中阶段的大多数定义和定理并不复杂,同学们从现在就应该养成精读并用数学语言准确理解概念和定理的习惯,这对于大家后续在高中和大学数学的学习十分重要。我们本质教育李泽宇三招TM的第一招就叫做翻译,就是在解题的时候把中文翻译成数学语言,同时在合适的时候在不同的数学语言之间进行互译。没有了良好的基础,这一招就成了空中楼阁,正所谓巧妇难为无米之炊。
如何检验自己的基础概念是否扎实?
费曼学习法
这是大物理学家费曼提出来的学习方法。现阶段,不要求大家使用类比等思维方式深层次地理解每一个概念背后的逻辑然后表达得连一个小学生也听得懂,你只需要这样做:
用自己的话,在一分钟内把概念或者定理复述一遍。然后利用录音,QQ录音等录下来,之后对比你讲的和教科书上的内容。如果一致,那么就说明你懂了,如果不一致,或者说不清楚,说不出来,那么不好意思,你这个概念掌握得比较差。
我非常相信王阳明先生的“知行合一”四个字,知而不行就是未知。在你运用这些概念之前,最起码的“行”就是能够说得出来,连说都说不出来,谈什么知呢?
3. 盲目做题,刷题,不去体悟数学思维 – 解决问题之道
最开始我成立本质教育并只教授高中数学,是因为我认为现有的高中数学教育是非常有问题的:数学变得死记硬背,学生没有学到创造性的解题(解决他们从所未见的问题)的思维和能力,从而导致长大了容易“高分低能”。(我在汇丰工作期间,遇到的一些从世界一流大学毕业的孩子,做老师教过的,老板教过的问题,勤勤恳恳。但要他们给他们一个探索性的项目,往往无从下手。)
我本来以为初中的数学(至少中考难度的数学)比较简单,用不了多少数学思维,因此一直没有开设初中课程。但有很多家长找到我们,迫切希望我们开设初中课程。等我实际开始做最近这几年的中考题,发现至少在平面几何上,一些中考的压轴题并不简单(至少不比高考题目简单),对数学思维也有了一定的要求。因此,我们也开设的初中课程,并从初中就将数学思维教授给同学们。随着我接触的初中孩子越来越多,我也越来越发现这么做的必要性。
这一部分内容较多,也比较抽象,不可能用一篇文章就概括了,我现在就用一道中考平面几何题来谈数学思维 – 李泽宇三招TM的一部分运用:
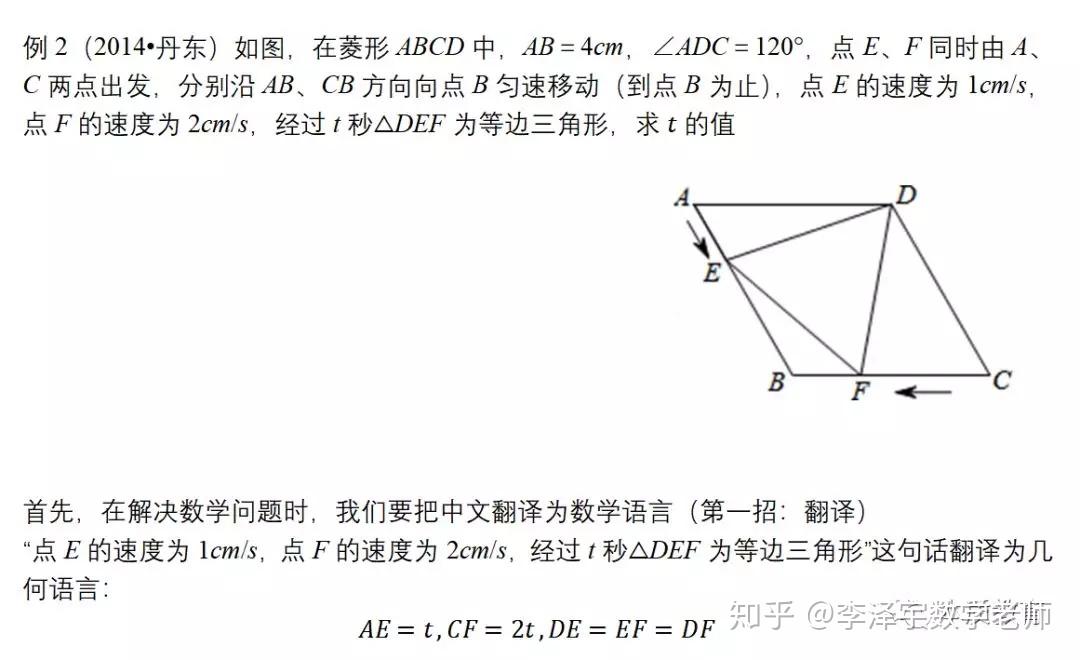

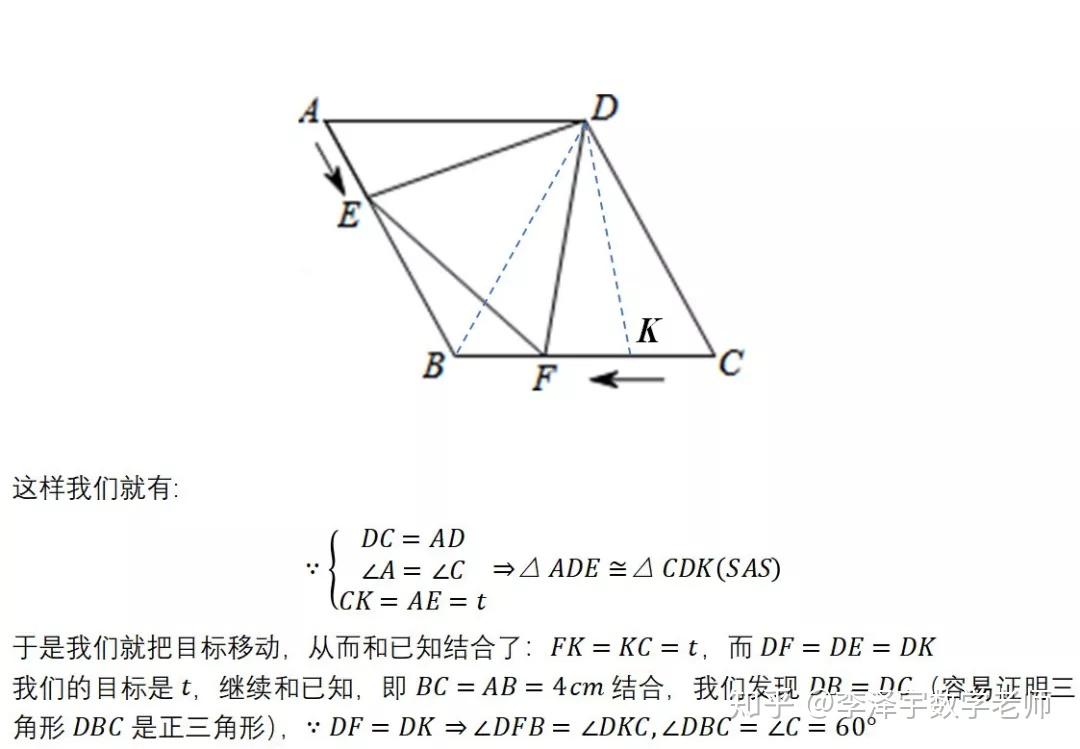
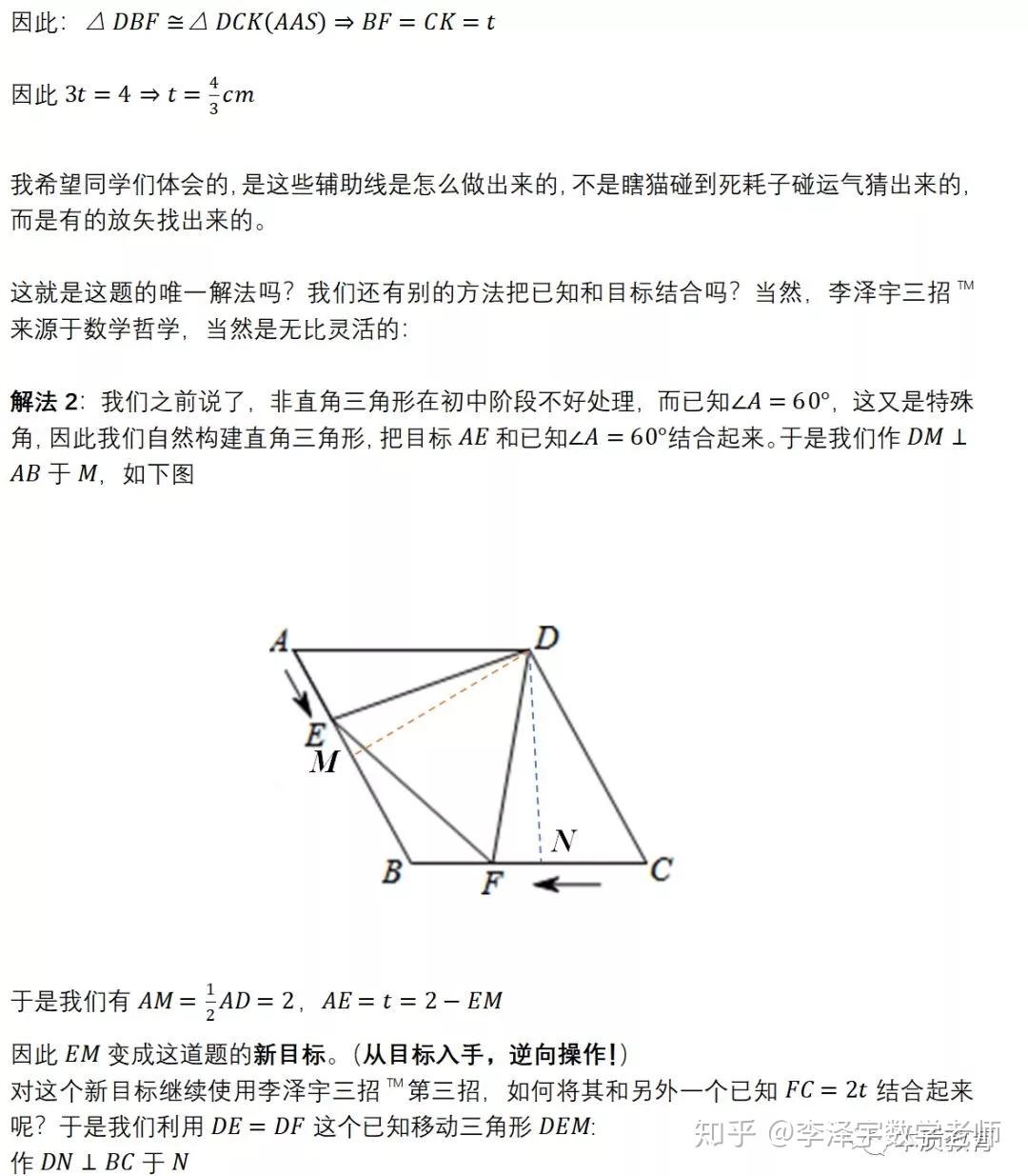
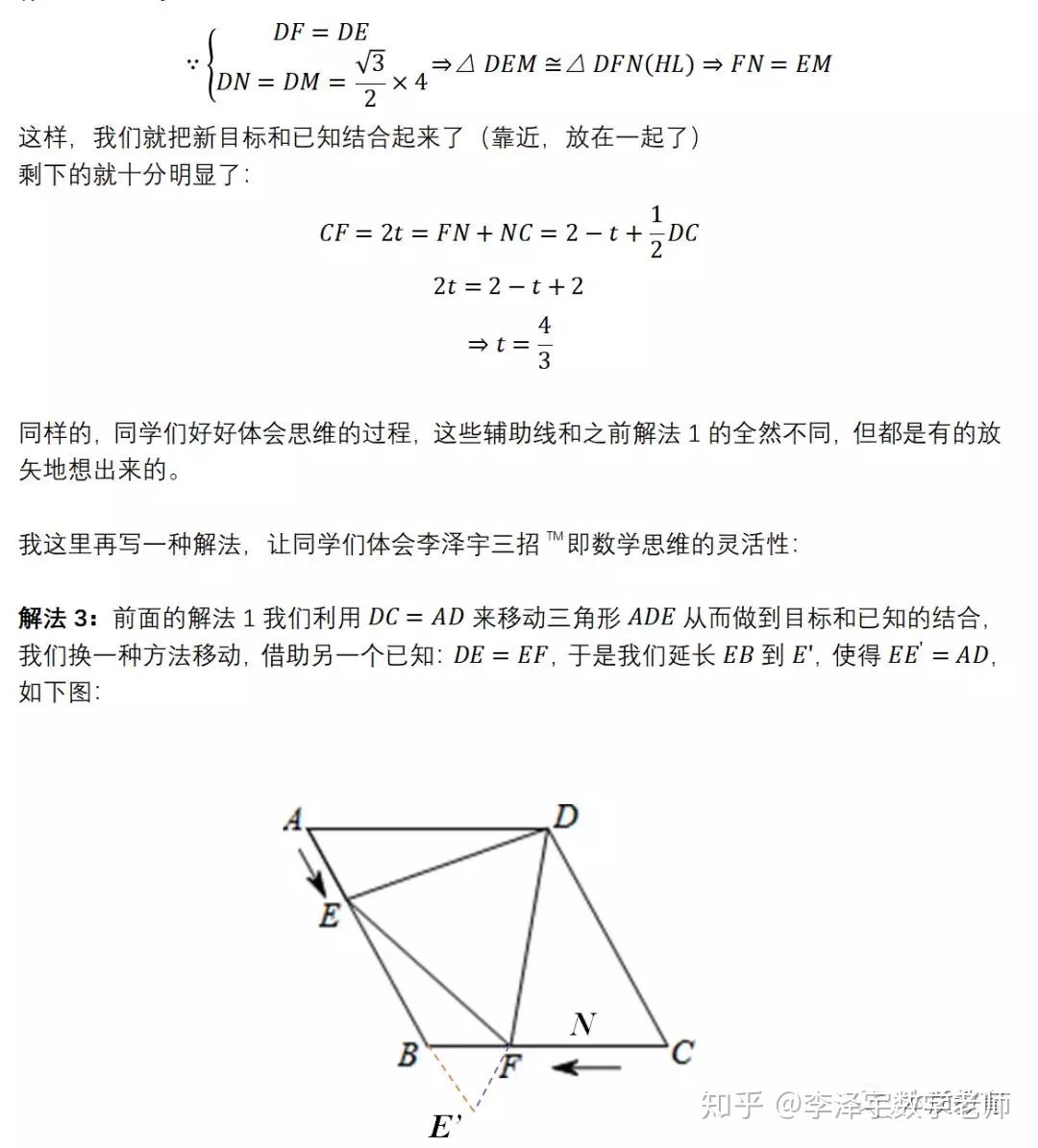

4. 不会从错误中学习
我先定义以下什么是错题:
1. 做错的题(包括3种:粗心,概念不清,以及逻辑问题,这三者一定要严格区分开来)
2. 不会做的题
3. 做得慢,没有在规定时间做完的题
这些都是你的错题。
很多同学遇到错题,就扫一遍答案,看懂了,然后?然后就没有然后了。
这样的学习,恕我直言,你是在浪费题目和时间!这样日积月累,你表面上很努力,不过只是在重复做无用功罢了。
据我的观察,很多同学很努力,但是他们的进步曲线是平的,如下图:
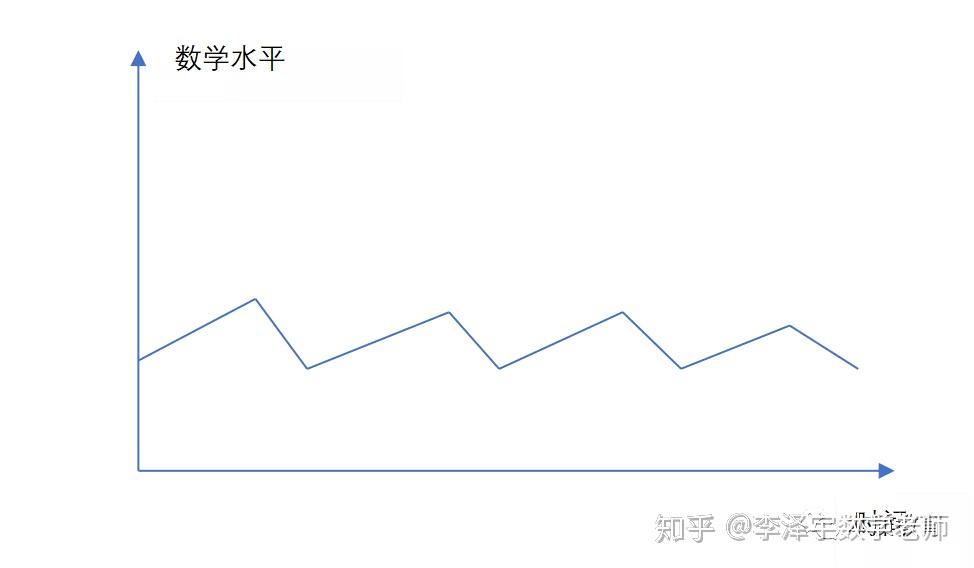
他们无非是不断地跌落在同样的坑里面吧了。说得难听些,这个叫做伪勤奋。
请记住:错误是一个人最大的学习之源!
我的一生最重要的原则,方法都是从错误(自己的+别人的)中学来的。正如孟子所言,闻过而喜。(我现在还没有达到他的程度,出现问题我往往还是比较不爽的,达不到“喜”的程度)
那么如何从错误中学习呢?我总结了以下反馈环

遇到错误,首先的就是要找原因。例如上面的例2,若你做不出来,你要问自己:
1. 为什么我做不出来,是数学思维(李泽宇三招TM)哪一点没有掌握好?
2. 我能用自己的话说出这第三招吗?
3. 我能够遮住答案,模仿老师的思维,把这一题用三种方法解出来吗?
4. 我能用老师没说过的方法求解出来吗?
这样,你每一题就会得到进步。1题,2题…10题,100题,扎实的数学基础+数学思维不就是你的囊中之物了吗?何愁考试考不好?
5. 知行合一
知而不行就是不知!一部分同学说:老师你讲得太好了,我一定努力跟着学习。一个月以后问他,你研究了几道错题呀?用了费曼学习法把每个概念用自己的话说一遍了吗?
回答:……
你现在明白你为什么数学成绩提不高了吗?