鸟群在飞行时是否会发生碰撞?如果不会,它们之怎样协调的?这种原理能否运用于无人驾驶?
恭喜你,这个小小的奇思妙想已经摸到了算法工程师甚至诺奖级别的门槛。
不过很可惜你想到得有点晚了。
由鸟群飞行启发而来的算法已经在用了,而且用了快40年了,现在也广泛应用于无人机等领域。
1986年的某天,Symbolics公司的算法工程师Craig Reynolds盯着窗外群鸟盘旋却没有撞在一起,突然灵光一闪——那些在空中优雅转身的鸟群,不正是天然的自组织算法吗?
这位"数字鸟群之父"当即敲下代码,让屏幕上的虚拟鸟(Boids)第一次像真实生物般聚散飞行。

让人意想不到的是,这个最初用在《蝙蝠侠》电影特效的算法,竟成了未来各种AI算法的"种子"!
Craig的Boids模型,这个优秀的算法在随后30年后引领各种算法界的"智能革命"。
1995年,其他算法工程师们受他启发,将Boids升级为粒子群算法(PSO),如今你的手机导航、无人机编队在空中跳起华尔兹,背后都是这些"数字候鸟"在指挥!
从大银幕特效到改变现实世界的黑科技,这群"数字鸟"教会我们:最精妙的算法,有可能藏在大自然里。
无独有偶,2021年的诺奖物理学家乔治·帕里西曾经也做过鸟群飞行的研究。
受鸟群的启发,在复杂系统的研究里大放异彩,最主要工作是给出了平均场自旋玻璃模型(SK模型)的严格解,因为预测复杂系统的长期行为的贡献,最终获得诺奖。
(他的科学方法论写在《随椋鸟飞行》一书当中了,感兴趣的可以看看)
下次仰望天空时,说不定你也能从飞鸟轨迹里破译出改变世界的密码呢!
好的,那么我们还是回到鸟群,一窥这来自于奇妙的自然界的算法吧。


这是一个鸟群短短几十秒的飞行轨迹,可以看出,虽然鸟群的数量非常庞大,但是它们竟然能井然有序地让鸟群合拢然后分开。
事实就是,大多数时候鸟群之间都能互相协调,不会发生碰撞,偶尔碰撞那是比较少见的情况。
那么鸟类是如何做到这一点的呢?
这里我们先引入一个小小的基本概念:
涌现:
当大量简单个体通过相互作用形成复杂系统时,系统整体展现出个体无法单独实现的新特性或行为。这些特性无法通过简单叠加个体行为预测,而是源于个体间非线性的动态关系。
一只鸟+一只鸟=两只鸟
但是鸟群≠100只鸟简单相加。
正如音乐之于贝多芬,三个音加在一起是一个和弦,但是和弦加在一起不是更多的和弦,而是命运,是星辰。
涌现现象就是这么神奇。下面举一些生活中涌现的现象方便理解。
比如磁铁,单个原子仅具微小磁矩,但整块的磁铁里原子的自旋自发对齐,形成宏观磁性。单独原子无此特性。这种现象被称为自发磁化。
比如意识,单个的蛋白质没有意识,组成的细胞也没有意识,但是大量细胞组成的人体会涌现出意识,这是蛋白质层面没有的特性。
那么鸟类是怎么实现这种群体行为的呢?
省流版总结:鸟并不清楚自己在鸟群的位置,它们不是整体协调的,它们只关注自己附近大约6-7只鸟的相对位置。
刚才提到的诺奖得主乔治·帕里西曾用距离几十米的三架高清全画幅相机同时以毫秒的精度每秒拍摄五张照片,实际上,他们在每个机位上都安装了两台相互连接的设备,它们可以交替拍摄,使图像频率翻倍,所以我们其实每秒拍摄了10帧图像。
最终共收集了约500个群聚事件,但只有50个事件满足三维重建的条件。他们最后选择了10个具有清晰边界、强空间凝聚力和大量鸟群的事件进行分析。
这是乔治·帕里西的论文*1:
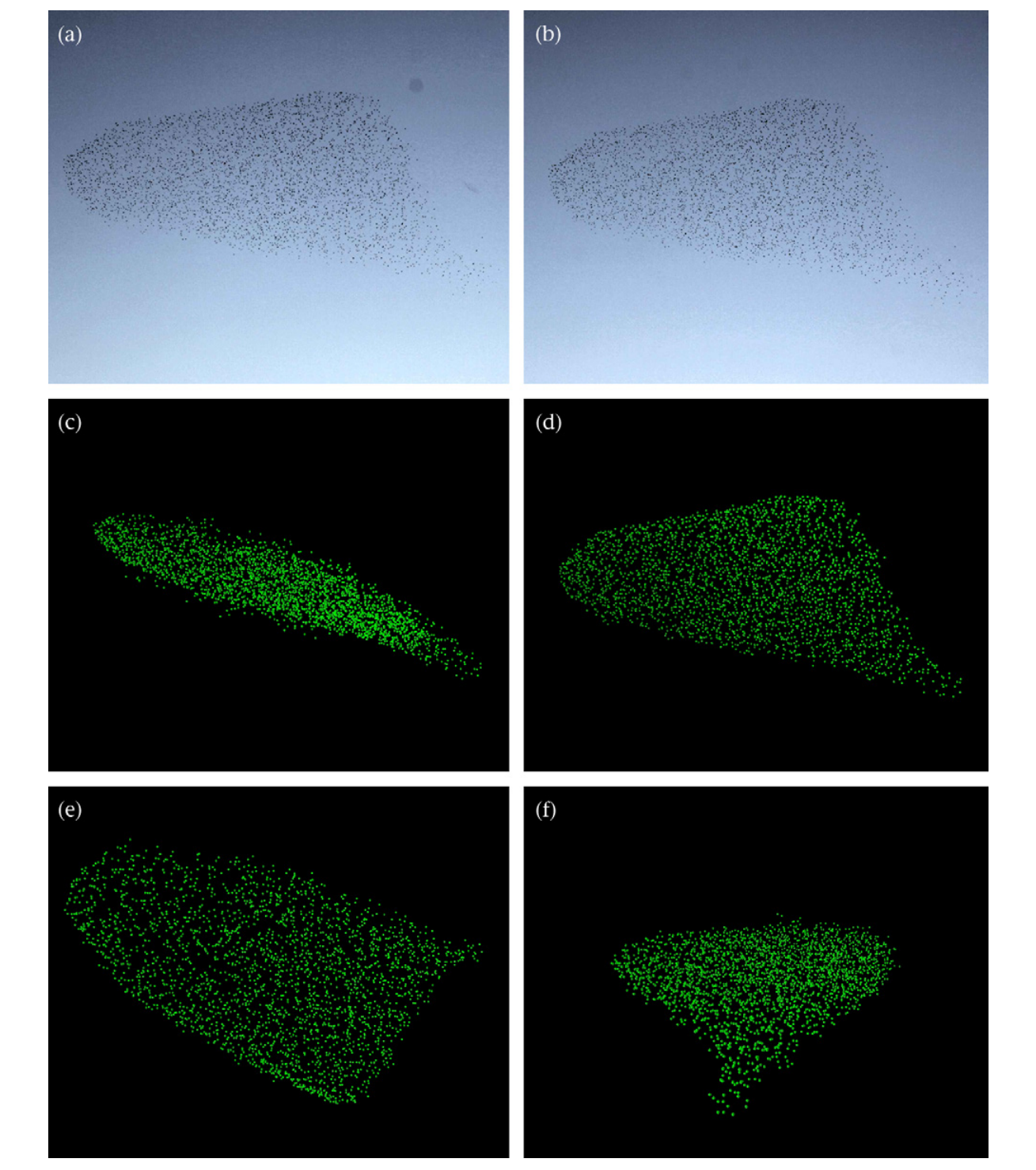
最终他们通过一系列三维重建分析和建模得出来如下结论:
1鸟群有特定的形状,即在竖直方向上较薄,在水平方向更密集。
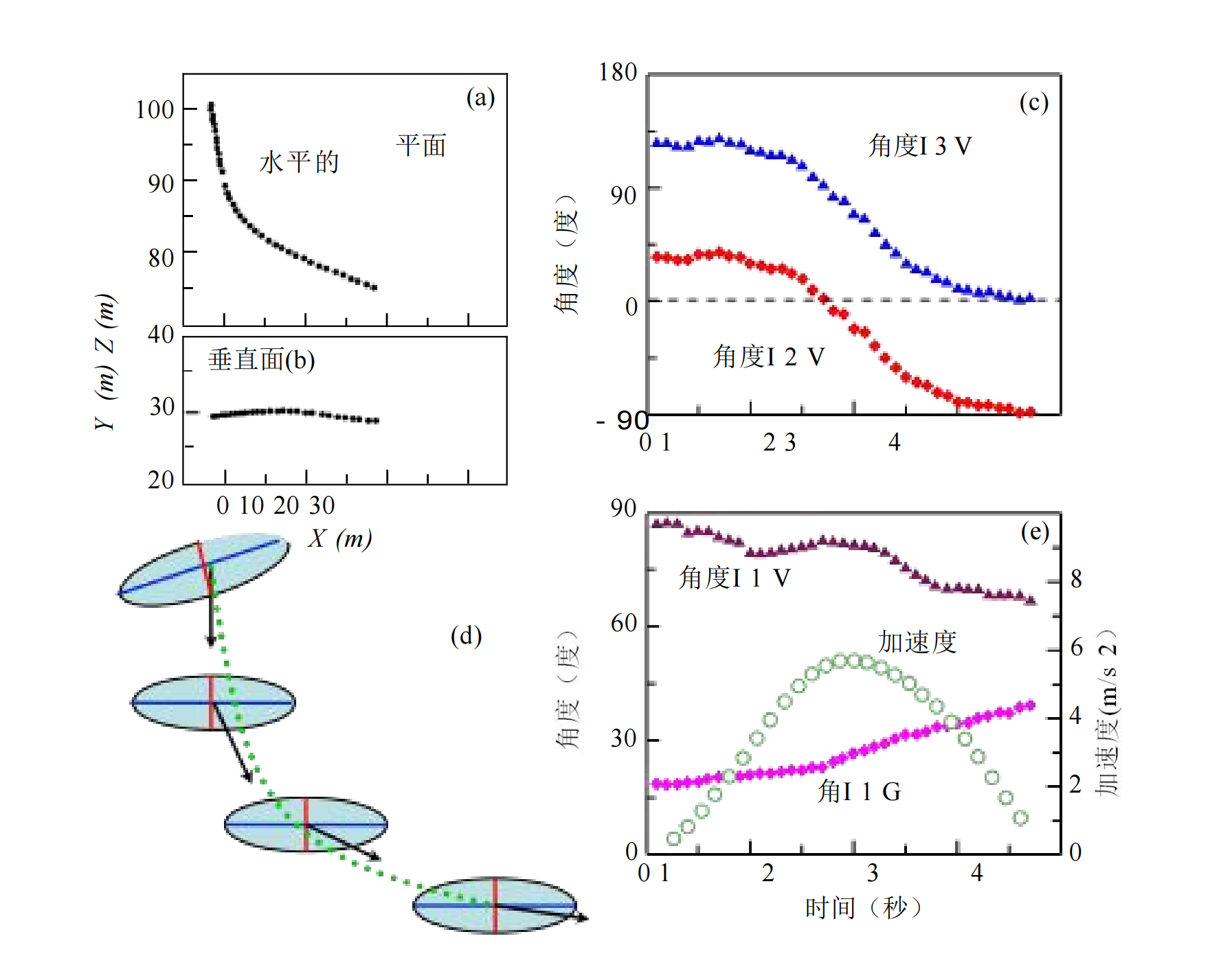
2方向性:所有分析的鸟群在空间中都有明确的方向性,速度的方向和重力大致垂直,而偏航角和重力几乎平行。
这意味着鸟群在水平方向上移动,几乎平行于地面飞行。
转向行为:在转向过程中,鸟群相对于速度的方向发生了变化。
如果鸟群最初沿着中间轴移动,在转向结束时,它会沿着最长轴定向。
密度变化:所有鸟群内部都存在密度梯度,即边界处的密度高于中心。
具体到单个鸟的行动:
单只鸟只关注它附近6-7只鸟,保证自己跟它们不相撞就行。
这就说明鸟类之间的相互作用依赖于拓扑距离而非度量距离。
拓扑距离:鸟只关注最近的6-7只鸟,无论他们距离0.5米还是3米(固定邻居数量)。
这样做的好处是:每只鸟始终追踪最近的7只邻居,无论它们飞得近还是远。当群体扩张时,实际距离拉大但互动数量不变,群体依然能同步转向。
假如设定只关注3米内的鸟,当群体扩散到间距5米时,互动中断会导致群体解体。
至于为什么是6-7个?
这里就涉及到一个很有趣的感数的概念。
感数subitizing:
要更好地理解这个问题,我们先来看这幅图:

图中的这些骰子点数是多少?
你会发现,对于有些骰子你一眼就能看出点数,而有些骰子则需要数一数才能确定点数。
人和一些动物天生就具有一种能力,能一瞬间识别出一些小数量物体的数量。
这个概念叫做感数(或瞬时知觉)(subitizing),一般来说,没经过训练的普通人感数最大值是4(一般不超过5)。
这一概念由E.L. Kaufman等人在1949年提出,源自拉丁词“subitus”,意为“突然”。当物体数量超过四个或五个时,观察者通常需要借助计数或熟悉的模式(如骰子上的点数排列)来确定数量。
研究表明,在瞬时知觉范围内(1-4个物体),人们的判断速度快、准确率高且充满信心。然而,当数量超出此范围,判断的准确性和信心会下降,反应时间显著增加,每增加一个物体,额外耗时250-350毫秒。
所以对椋鸟来说,它们的感数是6-7,这个是不需要数数,一眼就能看出来的数量,它们只关注感数范围内的鸟就可以了~
有趣的是,无人机的龙头大疆,也采用了类似生物的双目视觉避障法来指导无人机的避障:
双目视觉的基本原理是利用两个平行的摄像头进行拍摄,然后根据两幅图像之间的差异(视差),利用一系列复杂的算法计算出特定点的距离,当数据足够时还能生成深度图。

人类等生物也是用双目视觉来计算物体跟自己的距离的。
这个比红外等依靠物体表面反射的探测方法好用。
回到鸟群,经过刻意训练后,椋鸟的这种协调性可以达到惊人的百毫秒级别。
Pomeroy和Heppner曾经在1977在实验室*2中对椋鸟进行过实验,鸟类对光刺激的平均反应时间为76.38毫秒,对声音刺激的平均反应时间为80.64毫秒,而鸟群转向传播到整个群体只需要140ms左右。
达到惊人的协调性,仿佛一个鸟群就是一个整体。
要知道,普通人的反应速度是150-300毫秒(视觉约200ms,听觉约150ms),经过训练的运动员才能达到100毫秒级别。
好了!现在你知道鸟类是如何转向的了。
那么已经有了理论支撑,我们现在可以写代码了。
Boids是克雷格·雷诺兹 Craig Reynolds 在1986年开发的一个用来模拟鸟类群体行为的计算机程序。“ boid”是“ bird-oid object”的缩写,是指类鸟程序。
与大多数生物启发的智能算法程序一样,Boids也是涌现现象的一个例子*3。
换句话说,Boids的复杂性不是因为Craig Reynolds给它设定了超级复杂的算法,而是基于一些简单规则让程序里面的个体有了现实生活中真实生物一般的复杂性:
他只给程序里的粒子设定了这三条基本规则:
1. 避免碰撞:避免与附近的群体成员发生碰撞
2. 速度匹配:尝试与附近的群体成员匹配速度
3. 集群中心化:尝试靠近附近的群体成员
其中速度是矢量,包含了速度的方向和大小。
就这简单的三条规则,引领了后续几十年各种风骚的遗传算法。目前论文引用量已经上万了:

后续的很多模型都遵循或使用了这些规则的变体。
比如刚才提到的粒子算法
自推进粒子模型(SPP):1995年,物理学家Tamás Vicsek团队从1986年Craig Reynolds的鸟群模型(Boids)中提炼出一个简化版本:
核心规则:一群以恒定速度移动的"点粒子",每隔一段时间就会根据周围邻居的平均运动方向调整自己,并叠加一点随机扰动(类似人类走路时的无意识晃动)。
这种模型具有惊人的团队协调性,只要设定"最近邻规则"(例如每颗粒子只关注半径2米内的同伴),即使没有中央指挥系统,所有粒子最终会统一行动——要么聚集成团,要么同步朝同一方向移动。
其实现实生活中很多生物都是自推进粒子,鸟群、鱼群、羊群等等。生物群体看似简单的跟随规则,实则是亿万年进化出的最优分布式决策系统。
想象一下这样的场景:
如果让一群遵守SPP规则的行人通过狭窄通道,你觉得他们会自发形成单向流动还是持续拥堵?实验证明,当通道宽度小于3倍人体肩宽时,系统会进入"双向交替通行"的稳定状态——这或许能解释为何地铁换乘通道左右分流就可以避免堵塞,因为这是一种非常自然的解法。
然后还有粒子群优化算法(PSO)也是受此启发的。
这个算法在粒子群模型上进行了优化,它使用随机优化 Stochastic optimization方法不断迭代搜索,以找到局部最佳值,然后把这个值推广到其他粒子。
PSO相比传统穷举法,计算量减少90%。
现在的无人机避障的智能算法里,就有很多受生物启发的算法,比如:
遗传算法、蚁群算法、还有刚才提到的粒子群算法(PSO)*4等等。
所以现在已经应用于无人机了,以后等无人驾驶技术成熟了,应用于无人驾驶技术也未尝不可。
另外,国家现在开始布局低空经济,以后低空载人飞机应用鸟群启发的粒子群优化算法(PSO)也是刚好的,毕竟都是飞行器,行为也有相通的地方。
以上~
1Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study
2Laboratory determination of startle reaction time of the starling (Sturnus vulgaris)
3Flocks, Herds, and Schools: A Distributed Behavioral Model
4无人机集群路径规划算法研究综述 刘君兰,张文博,姬红兵,朱明哲
5失控 凯文·凯利
6群体行为 - 集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织