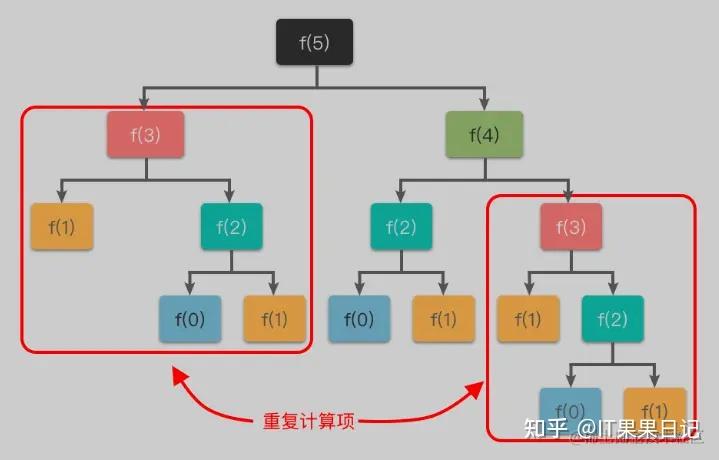
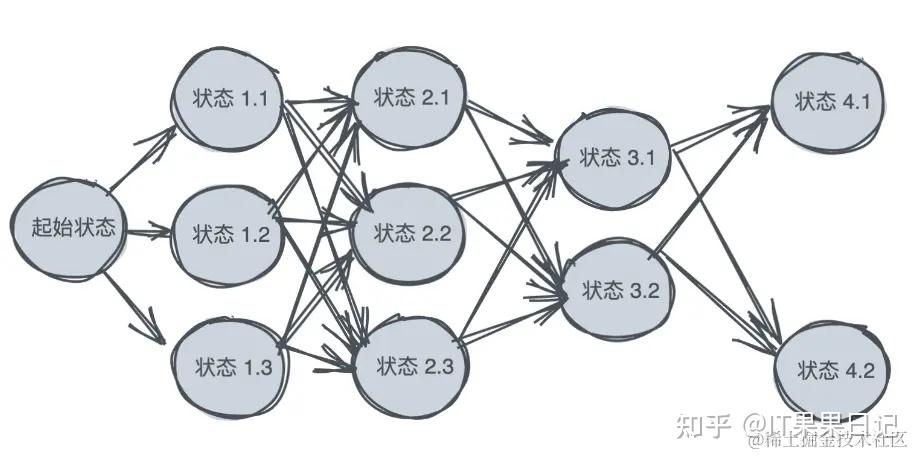
如何通俗理解动态规划算法呢?
动态规划中的状态转移方程设计与优化
动态规划(Dynamic Programming,DP)是一种用于解决复杂问题的算法设计方法,特别适用于那些可以被分解成子问题的情况。其核心思想是通过将问题拆分成更小的子问题,并将子问题的解存储起来以避免重复计算。动态规划的关键在于设计高效的状态转移方程,并进行适当的优化,以提升算法的性能。
本文将深入探讨动态规划中的状态转移方程的设计与优化,结合具体的代码实例,帮助读者更好地理解如何构建和优化动态规划算法。
状态转移方程的设计
在动态规划中,状态转移方程(或递推公式)用于描述一个状态如何从之前的状态转移而来。设计状态转移方程的步骤通常包括:
- 确定状态:定义一个或多个状态变量,这些变量能够充分描述子问题的解。例如,在求解最长公共子序列(LCS)问题时,可以定义状态
dp[i][j]表示前i个字符的第一个字符串和前j个字符的第二个字符串的最长公共子序列长度。 - 定义状态转移方程:根据问题的特性,定义当前状态如何由先前状态转移而来。这通常涉及到对状态变量的操作,例如选择、合并或比较。
- 初始化:设置边界条件和初始状态,确保算法的正确性和完整性。
- 计算顺序:根据状态转移方程的依赖关系,确定状态计算的顺序,以确保所有需要的子问题都已计算完成。
状态转移方程设计实例
以背包问题为例,讨论如何设计状态转移方程。
背包问题简介
给定 n 个物品,每个物品有一个重量 w[i] 和一个价值 v[i],以及一个最大承载重量 W 的背包。目标是选择一些物品放入背包,使得背包内的总价值最大化。背包问题可以通过动态规划来解决。
状态定义
定义 dp[i][j] 为前 i 个物品中,在容量为 j 的背包中能获得的最大价值。
状态转移方程
- 选择第
i个物品:如果我们选择第i个物品,则背包的容量减少为j - w[i],同时增加的价值为v[i],因此: [dpi[1] = dpi-1[2]] + v[i]] - 不选择第
i个物品:如果我们不选择第i个物品,则背包的容量保持不变,价值为dp[i-1][j]: [dpi[3] = dpi-1[4]]
综合以上两种情况,状态转移方程为: [dpi[5] = \max(dpi-1[6], dpi-1[7]] + v[i])]
初始化
dp[0][j] = 0:没有物品时,无论背包容量是多少,最大价值均为 0。dp[i][0] = 0:背包容量为 0 时,无论有多少物品,最大价值均为 0。
代码实现
以下是背包问题的 Python 实现:
def knapsack(weights, values, W):
n = len(weights)
# 初始化 dp 数组
dp = [[0] * (W + 1) for _ in range(n + 1)]
# 填充 dp 数组
for i in range(1, n + 1):
for j in range(1, W + 1):
if weights[i - 1] <= j:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
else:
dp[i][j] = dp[i - 1][j]
return dp[n][W]
# 示例
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
W = 5
print(knapsack(weights, values, W)) # 输出 7
状态转移方程的优化
动态规划的性能可以通过以下几种方式优化:
- 空间优化:许多动态规划问题的空间复杂度可以通过优化状态存储方式来减少。例如,背包问题中,状态
dp[i][j]只依赖于前一行的状态dp[i-1][*],因此可以用滚动数组来优化空间复杂度。 - 状态压缩:在某些问题中,可以压缩状态空间,通过合并状态变量或减少不必要的状态存储来优化。
- 记忆化搜索:对于某些动态规划问题,可以使用递归加上记忆化技术来避免重复计算,从而优化性能。
代码优化示例:空间优化
以下是背包问题的空间优化版代码:
def knapsack(weights, values, W):
n = len(weights)
# 初始化一维 dp 数组
dp = [0] * (W + 1)
# 填充 dp 数组
for i in range(n):
for j in range(W, weights[i] - 1, -1):
dp[j] = max(dp[j], dp[j - weights[i]] + values[i])
return dp[W]
# 示例
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
W = 5
print(knapsack(weights, values, W)) # 输出 7
动态规划的高级优化技巧
在动态规划的实际应用中,除了基本的空间和时间优化外,还有一些更高级的优化技巧,可以进一步提高算法的效率。这些技巧包括:
- 双指针法:有些问题可以通过双指针法优化状态转移的计算。例如,在处理一些区间问题时,可以使用双指针来减少计算量。
- 优先队列:对于某些需要在状态之间进行优先级选择的问题,可以使用优先队列(如最小堆或最大堆)来加速状态转移过程。
- 启发式搜索:结合启发式搜索方法(如 A* 搜索)与动态规划,可以在解决一些复杂问题时提高效率。例如,在路径规划问题中,启发式搜索可以用来快速定位可能的最优解。
- 约束条件:通过分析问题的约束条件,往往可以进一步优化状态转移方程。例如,通过将某些无效状态或不必要的计算排除在外,可以显著提高算法的效率。
代码示例:双指针法优化

以最长上升子序列(LIS) 问题为例,介绍如何使用双指针法优化状态转移。
问题描述:给定一个整数数组 nums,找出其中最长上升子序列的长度。可以使用动态规划来解决这个问题,但在某些情况下,使用双指针法可以提高效率。
优化思路:使用一个 tails 数组,其中 tails[i] 表示长度为 i+1 的上升子序列的最小尾部值。通过二分查找来更新 tails 数组,进而优化状态转移。
import bisect
def lengthOfLIS(nums):
if not nums:
return 0
# tails 数组
tails = []
for num in nums:
# 使用二分查找找到当前 num 应该插入的位置
index = bisect.bisect_left(tails, num)
# 如果 num 大于 tails 中所有元素,则添加到 tails 末尾
if index == len(tails):
tails.append(num)
else:
# 否则,更新 tails 中的值
tails[index] = num
return len(tails)
# 示例
nums = [10, 9, 2, 5, 3, 7, 101, 18]
print(lengthOfLIS(nums)) # 输出 4(最长上升子序列是 [2, 3, 7, 101])
动态规划与其他算法的结合
在许多实际应用中,动态规划往往与其他算法(如贪心算法、回溯算法等)结合使用,以获得更高效的解法。了解这些结合方法能够帮助解决更复杂的问题。
- 动态规划与贪心算法:有些问题可以先使用贪心算法进行初步解决,再结合动态规划进行优化。例如,在解决最小生成树问题时,贪心算法可以找到一个初步解,动态规划则可以用于进一步优化。
- 动态规划与回溯算法:在某些情况下,回溯算法可以用于生成所有可能的解,而动态规划则可以用于存储和优化这些解。例如,在求解背包问题时,可以使用回溯算法生成所有可能的物品组合,再通过动态规划优化解的计算。
- 动态规划与分治法:有些问题可以使用分治法将问题分解成子问题,子问题的解可以通过动态规划进行求解。例如,在解决矩阵链乘法问题时,分治法和动态规划可以结合使用,以优化计算过程。
实际应用中的动态规划
动态规划不仅在算法竞赛和学术研究中有广泛应用,也在实际生产环境中发挥着重要作用。例如:
- 财务规划:在投资和财务规划中,动态规划可以用于制定最佳的投资策略和预算分配方案。
- 网络流量优化:在网络流量管理中,动态规划可以用于优化数据包的传输路径,减少延迟和拥塞。
- 基因序列分析:在生物信息学中,动态规划可以用于分析基因序列,寻找最长的公共子序列等。
通过对动态规划的深入理解和优化,可以更好地解决实际问题,提高算法效率,从而在各种应用场景中获得更好的结果。
高级动态规划问题分析
在掌握了基本的动态规划算法设计与优化技巧之后,我们可以进一步探讨一些更复杂的动态规划问题,这些问题通常具有特殊的性质或额外的约束。以下是一些高级动态规划问题的分析和解决策略。
1. 带权图中的最短路径问题
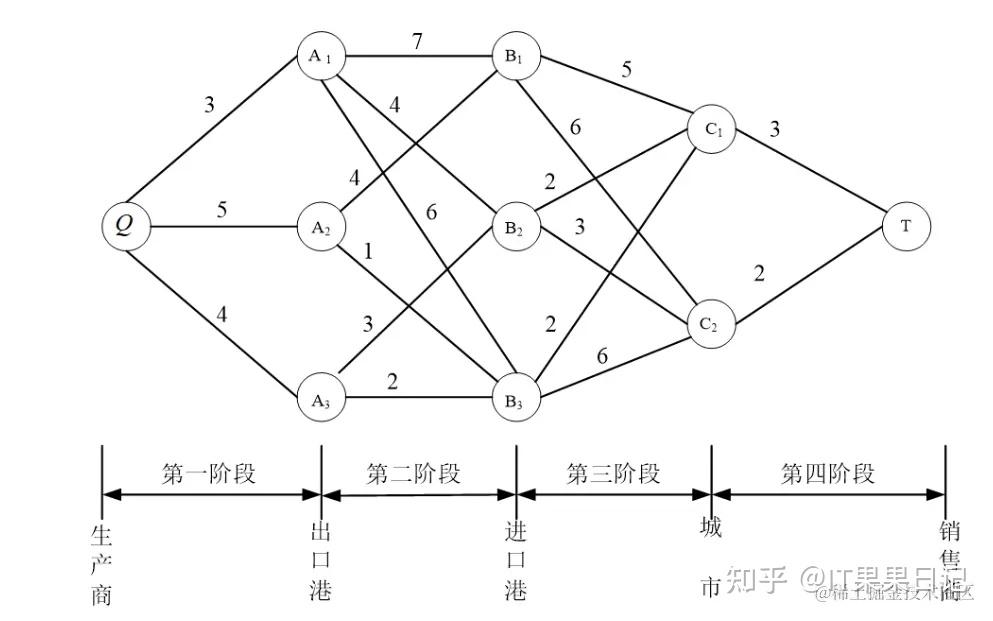
在带权图中寻找最短路径是一个经典问题,可以使用动态规划方法进行优化。例如,Floyd-Warshall 算法用于计算图中所有节点对之间的最短路径。该算法的时间复杂度为 (O(n^3)),适用于小规模图,但在大规模图中可能需要更高效的算法。
Floyd-Warshall 算法的状态转移方程如下: [dpk[8][j] = \min(dpk-1[9][j], dpk-1[10][k] + dpk-1[11][j])] 其中,dp[k][i][j] 表示使用前 k 个节点作为中介的最短路径。
代码示例:
def floydWarshall(graph):
n = len(graph)
# 初始化 dp 数组
dp = [[float('inf')] * n for _ in range(n)]
# 初始化边权
for i in range(n):
for j in range(n):
if i == j:
dp[i][j] = 0
elif graph[i][j] != 0:
dp[i][j] = graph[i][j]
# Floyd-Warshall 算法
for k in range(n):
for i in range(n):
for j in range(n):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j])
return dp
# 示例图(邻接矩阵)
graph = [
[0, 3, float('inf'), float('inf'), float('inf'), 10],
[float('inf'), 0, 2, float('inf'), float('inf'), 7],
[float('inf'), float('inf'), 0, 1, float('inf'), 6],
[float('inf'), float('inf'), float('inf'), 0, 4, float('inf')],
[float('inf'), float('inf'), float('inf'), float('inf'), 0, 2],
[float('inf'), float('inf'), float('inf'), float('inf'), float('inf'), 0]
]
distances = floydWarshall(graph)
for row in distances:
print(row)
2. 多维动态规划
在某些问题中,状态空间不仅仅是一个一维数组,而是一个多维数组。例如,编辑距离(Edit Distance) 问题,通常用二维 DP 数组解决,用于计算将一个字符串转换为另一个字符串所需的最少操作数(插入、删除、替换)。
编辑距离的状态转移方程: [dpi[12] = \min(dpi-1[13] + 1, dpi[14] + 1, dpi-1[15] + (s1[i-1] \neq s2[j-1]))] 其中,dp[i][j] 表示将 s1 的前 i 个字符转换为 s2 的前 j 个字符的最少操作数。
代码示例:
def minDistance(word1, word2):
m, n = len(word1), len(word2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m + 1):
dp[i][0] = i
for j in range(n + 1):
dp[0][j] = j
for i in range(1, m + 1):
for j in range(1, n + 1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1)
return dp[m][n]
# 示例
word1 = "intention"
word2 = "execution"
print(minDistance(word1, word2)) # 输出 5
3. 路径计数问题
在一些网格或图中,可能需要计算从一个点到另一个点的所有路径数量。例如,网格路径问题中,从左上角到右下角的路径总数可以使用动态规划来解决。
状态转移方程: [dpi[16] = dpi-1[17] + dpi[18]] 其中,dp[i][j] 表示从 (0,0) 到 (i,j) 的路径数。
代码示例:
def uniquePaths(m, n):
dp = [[1] * n for _ in range(m)]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
# 示例
m, n = 3, 3
print(uniquePaths(m, n)) # 输出 6
动态规划的实际挑战与解决
在实际应用中,动态规划可能会遇到以下挑战:
- 状态空间过大:对于状态空间较大的问题,可以通过状态压缩、约束优化等方法来减少计算和存储的复杂度。
- 计算时间长:动态规划的时间复杂度可能较高,特别是对于大规模问题。可以通过算法改进、启发式方法等来优化性能。
- 动态变化的输入:对于动态变化的输入数据,可以结合增量更新和动态调整的技术来提高效率。
动态规划在不同领域的应用
动态规划的强大功能使其在多个领域中得到了广泛应用。以下是一些动态规划在实际应用中的具体案例和技巧。
1. 生物信息学中的序列比对
在生物信息学中,序列比对是比较两种生物序列(如 DNA、RNA 或蛋白质)的重要任务。动态规划常用于计算最优的序列比对,以找到两种序列之间的最佳匹配。
Smith-Waterman 算法用于局部比对,计算两个序列的局部最优对齐。其状态转移方程如下: [H(i, j) = \max ] 其中,(S(i, j)) 是两个序列中第
i 和第 j 个字符的得分,(d) 是罚分(gap penalty)。
代码示例:
def smith_waterman(s1, s2, match=3, mismatch=-3, gap_penalty=-2):
m, n = len(s1), len(s2)
H = [[0] * (n + 1) for _ in range(m + 1)]
max_score = 0
max_pos = (0, 0)
for i in range(1, m + 1):
for j in range(1, n + 1):
match_score = H[i - 1][j - 1] + (match if s1[i - 1] == s2[j - 1] else mismatch)
delete_score = H[i - 1][j] + gap_penalty
insert_score = H[i][j - 1] + gap_penalty
H[i][j] = max(0, match_score, delete_score, insert_score)
if H[i][j] > max_score:
max_score = H[i][j]
max_pos = (i, j)
return max_score, max_pos
# 示例
s1 = "GATTACA"
s2 = "GCATGCU"
score, pos = smith_waterman(s1, s2)
print(f"Score: {score}, Position: {pos}")
2. 金融领域的资产组合优化
在金融领域,动态规划被用来解决资产组合优化问题,以最大化投资回报或最小化风险。经典的资产组合问题(如 马科维茨均值-方差优化)可以通过动态规划来解决。
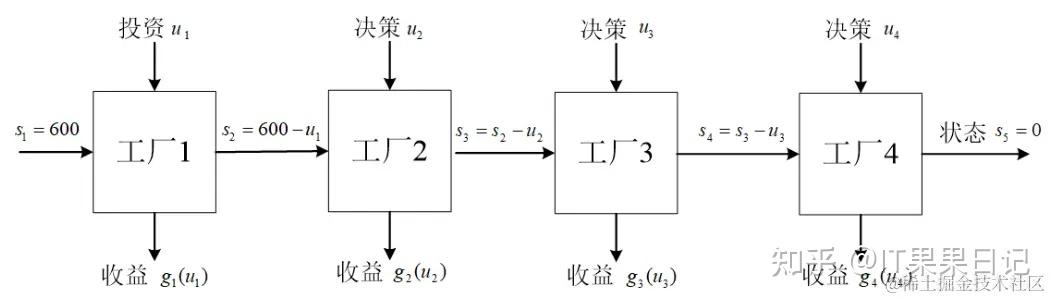
示例:假设有 n 种资产,每种资产的预期回报和风险(方差)已知,我们需要选择一个资产组合,使得预期回报最大化,同时风险最小化。
代码示例:
import numpy as np
def portfolio_optimization(returns, cov_matrix, target_return):
n = len(returns)
dp = np.zeros((n + 1, target_return + 1))
for i in range(1, n + 1):
for r in range(target_return + 1):
if returns[i - 1] <= r:
dp[i][r] = max(dp[i - 1][r], dp[i - 1][r - returns[i - 1]] + returns[i - 1])
else:
dp[i][r] = dp[i - 1][r]
return dp[n][target_return]
# 示例
returns = [5, 10, 15]
cov_matrix = [[0.1, 0.02, 0.03], [0.02, 0.2, 0.04], [0.03, 0.04, 0.3]]
target_return = 20
print(portfolio_optimization(returns, cov_matrix, target_return))
3. 智能交通系统中的路径规划
在智能交通系统中,动态规划用于解决路径规划问题,以优化交通流量和减少拥堵。例如,最短路径问题、旅行商问题(TSP)等可以通过动态规划算法来解决。
示例:旅行商问题中,寻找一个最短的回路,访问每个城市一次并返回起点。
代码示例(TSP):
import itertools
def tsp(graph):
n = len(graph)
all_points = range(n)
memo = {}
def dp(mask, pos):
if mask == (1 << n) - 1:
return graph[pos][0]
if (mask, pos) in memo:
return memo[(mask, pos)]
answer = float('inf')
for city in all_points:
if not mask & (1 << city):
answer = min(answer, graph[pos][city] + dp(mask | (1 << city), city))
memo[(mask, pos)] = answer
return answer
return dp(1, 0)
# 示例图(邻接矩阵)
graph = [
[0, 10, 15, 20],
[10, 0, 35, 25],
[15, 35, 0, 30],
[20, 25, 30, 0]
]
print(tsp(graph)) # 输出最短路径长度
4. 网络安全中的密码学应用
在网络安全中,动态规划可以用于解决密码学问题,例如计算最短的密钥生成时间,或优化加密算法的性能。
示例:字符替换密码的破解问题,动态规划可以帮助确定最短的密码破解路径。
代码示例(简单的字符替换密码破解):
def shortest_key_crack(original, encrypted):
m, n = len(original), len(encrypted)
dp = [[float('inf')] * (n + 1) for _ in range(m + 1)]
dp[0][0] = 0
for i in range(m + 1):
for j in range(n + 1):
if i > 0:
dp[i][j] = min(dp[i][j], dp[i - 1][j] + 1)
if j > 0:
dp[i][j] = min(dp[i][j], dp[i][j - 1] + 1)
if i > 0 and j > 0:
cost = 0 if original[i - 1] == encrypted[j - 1] else 1
dp[i][j] = min(dp[i][j], dp[i - 1][j - 1] + cost)
return dp[m][n]
# 示例
original = "key"
encrypted = "kex"
print(shortest_key_crack(original, encrypted)) # 输出最短破解长度
动态规划的未来趋势
随着计算机科学的发展,动态规划算法的研究不断进步,以下是一些未来的趋势和研究方向:
- 高维动态规划:随着数据维度的增加,传统的动态规划方法可能面临计算和存储的挑战。研究如何处理高维状态空间,优化计算和存储是一个重要的方向。
- 在线算法与动态规划结合:在处理实时数据时,如何将动态规划与在线算法结合,以便快速更新和调整,是一个重要的研究方向。
- 并行计算与动态规划:利用并行计算技术加速动态规划算法的计算,特别是在处理大规模数据时,能够显著提高算法的效率。
- 动态规划与机器学习结合:结合动态规划与机器学习技术,探索新的算法和模型,以解决更复杂的问题,特别是在处理不确定性和复杂环境下的问题时。
- 动态规划在新兴领域的应用:例如在量子计算、区块链技术等新兴领域,探索动态规划的应用潜力和挑战,以推动技术的发展。
总结
动态规划作为一种重要的算法设计技术,其应用范围广泛,包括生物信息学、金融优化、智能交通、网络安全等领域。通过深入理解和优化动态规划算法,结合实际问题的需求,可以有效解决各种复杂问题。在不断发展的计算机科学领域,动态规划仍然有着巨大的研究和应用潜力。希望本文的探讨能够为读者提供有价值的见解,帮助在实际应用中充分发挥动态规划的优势。
原文:https://juejin.cn/post/7396932633169559606
作者:申公豹本豹