单摆摆角大于 5° 时将作什么运动?
好的,让我们推导单摆一下在较大摆角下的运动方程。

考虑一个长为 ,质量为
的单摆,在重力作用下发生自由摆动。摆角 θ 与竖直线的夹角为正,重力
的分解可以表示为:
沿着摆动路径的分力:
垂直于摆动路径的分力:
根据牛顿第二定律,沿着摆动路径的运动方程为:
其中, 是摆动路径的弧长,
。因此,方程可以重写为:
我们可以简化这个方程,消去质量m,得到:
或者,重写为标准形式:
由于 在小角度下可以近似为
,但在
时,我们不能这么处理。此方程是一个非线性二阶微分方程,通常需要数值方法进行求解。
对于较大的角度,可以使用能量法来分析。单摆的机械能守恒,即势能和动能之和为常数:
其中, ,因此势能
。
将能量守恒式重写为:
可以从这个能量方程中求出 的表达式:
为了找到 ,可以进行分离变量的积分:
积分的复杂性取决于 的范围和具体情况,通常会涉及到椭圆积分或数值积分。
对于具体的数值解,建议使用数值积分方法,如 Runge-Kutta 方法,以获取 的时间演变。
我们可以通过泰勒展开式或摄动法来近似求解单摆的运动方程。
首先,我们考虑将 进行泰勒展开:
将其代入运动方程:
整理得:
这是一个非线性二阶微分方程,形式类似于简单谐振动,但有一个三次项。
在摄动法中,可以假设 的解为一个小参数
的级数展开:
将这个展开代入运动方程,得到每个级数项的方程。通常取 较小,使得
是近似的简谐解,考虑到高阶项对系统的影响。
对于简谐运动, ,解为:
对于第一阶摄动解 \( \theta_1(t) \),可以通过线性化后的方程求得。最终,近似解的形式为:
在小角度近似(泰勒展开)下,我们有:
以下 MATLAB 代码将实现数值解(使用 Runge-Kutta 方法)和近似解的比较,并绘制图形:
% 参数设置
l = 1; % 单摆长度
g = 9.81; % 重力加速度
theta0 = deg2rad(30); % 初始角度 (30°)
t_span = [0, 10]; % 时间范围
t_eval = linspace(0, 10, 100); % 评估时间点
% 数值解
% 运动方程的右侧
odefun = @(t, theta) [theta(2); - (g/l) * sin(theta(1))];
% 初始条件 [theta, omega]
initial_conditions = [theta0; 0];
% 求解
[t, theta_num] = ode45(odefun, t_span, initial_conditions);
% 近似解
theta_approx = theta0 * cos(sqrt(g/l) * t_eval);
% 绘图
p;
hold on;
plot(t, theta_num(:, 1), 'b-', 'DisplayName', 'Numerical Solution');
plot(t_eval, theta_approx, 'r--', 'DisplayName', 'Approximate Solution');
xlabel('Time (s)');
ylabel('Angle (rad)');
title('Comparison of Numerical and Approximate Solutions');
legend show;
grid on;
hold off;
运行以上代码后,将看到数值解(蓝线)和近似解(红虚线)的图形,通过观察两者的重合程度来验证近似解的正确性。
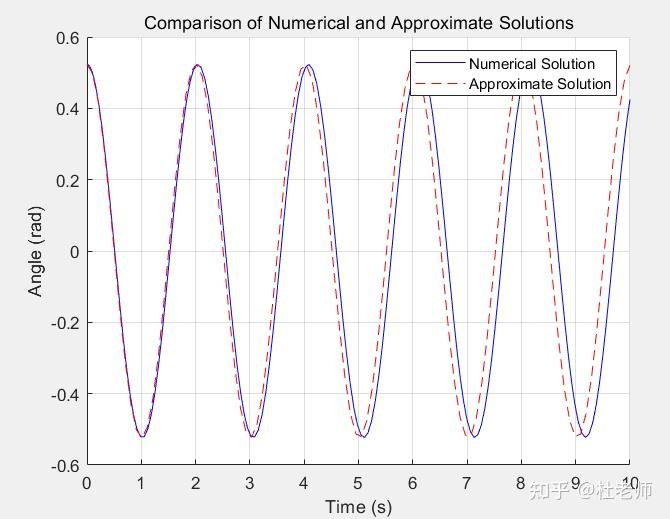
通过图形可以看出,当摆角较大时,运动方程中的非线性项使得系统的动力学行为变得复杂。尽管单摆在大角度下的运动是非线性的,但仍然表现出周期性特征。系统的运动周期会依赖于初始角度,较大的初始角度通常导致更长的周期。周期的变化使得单摆的行为与简单的简谐运动不同。
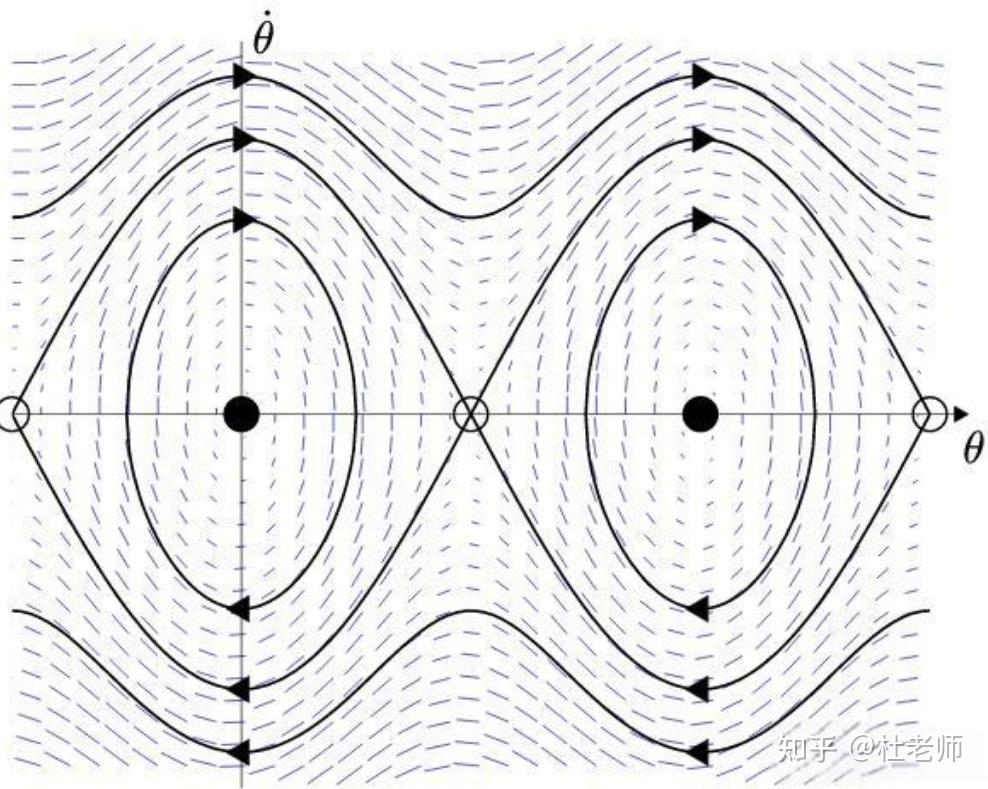
相图是描绘系统状态变化的重要工具。在相图中,横轴通常表示角度 ,纵轴表示角速度
。通过绘制相图,我们可以观察到:
在小角度近似时,相图中的轨迹是封闭的,表示周期性运动。随着角度增大,轨迹可能变得更加复杂。原点(静止位置)是一个不稳定的固定点,而 (倒立位置)是稳定的。摆动在相图中会表现出趋向于稳定点的行为。在某些情况下,随着初始条件的变化,系统可能表现出混沌行为,导致相图中的轨迹变得复杂而不规则。
在不同的相图区域,系统的能量分布不同,表现出不同的动能和势能特性。观察相图中轨迹的变化,可以识别出系统从周期性行为到混沌行为的转变。