将一个圆沿一个椭圆滚动一圈，圆心的轨迹是什么?

发布时间：

2024-12-20 11:20

阅读量：

先说结论：最后的结果应该是一个在实平面内包含两个分支的八次曲线，如果题主是高中生在教材的范围内这个问题其实没法做，我高中的时候试着考虑这个问题，后来才发现这个曲线次数还挺高的

回答：我们知道椭圆可以被参数化

$\displaystyle \left\{ \begin{array}{l} x = a\cos t\\ y = a \sin t \end{array} \right.$

对 $t$ 求导得到在 $(x_0, y_0) = (a\cos t_0,b\sin t_0)$ 处的一个切向量是 $(-a\sin t, b\cos t)$ ，所以向外的单位法向量为

$\displaystyle \frac1{\sqrt{b^2\cos^2 t_0 + a^2\sin^2 t_0}} (b\cos t_0, a\sin t_0)$

假设圆的半径为 $r$ 则圆心的参数方程为（如果只求参数方程其实这一步就够了，但是我们不妨把 $t$ 消掉直接得到一个关于 $x, y$ 的代数方程）

$\displaystyle \left\{ \begin{array}{l} x= \left(a + \dfrac{br}{\sqrt{b^2\cos^2 t + a^2\sin^2 t}}\right) \cos t \\ y = \left( b + \dfrac{ar}{\sqrt{b^2\cos^2 t + a^2\sin^2 t}} \right) \sin t \end{array} \right.$

做代换 $\displaystyle \left\{ \begin{array}{l} u = \cos t \\ v = \sin t\end{array} \right.$ ，则方程可以写为

$\displaystyle \left\{ \begin{array}{l} x= \left(a + \dfrac{br}{\sqrt{(b^2 - a^2) u^2 + a^2}}\right) u \\ y = \left( b + \dfrac{ar}{\sqrt{(a^2-b^2)v^2 + b^2}} \right)v \end{array} \right. \quad , u^2+v^2=1$

化简得到关于 $u,v$ 的多项式方程组

$\displaystyle \left\{ \begin{array}{l} [(b^2-a^2)u^2 + a^2](x-au)^2 - b^2 r^2 u^2 = 0 \\ [(a^2-b^2)v^2 + b^2](y-bv)^2 - a^2 r^2 v^2 = 0 \\ u^2 + v^2 - 1 = 0 \end{array} \right.$

通过求两次结式分别消去 $u,v$ 得到下面这个关于 $x,y$ 的很长的曲线方程

$\begin{array}{l} b^4 x^8 + (2 a^2 b^2 + 2 b^4) x^6y^2 + (a^4 + 4 a^2 b^2 + b^4) x^4y^4 +\\ (2 a^4 + 2 a^2 b^2) x^2y^6 + a^4 y^8 + \\ (- 4 a^2 b^4 + 2 a^2 b^2 r^2 + 2 b^6 - 4 b^4 r^2) x^6 +\\ (- 6 a^4 b^2 - 2 a^4 r^2 + 2 a^2 b^4 + 2 a^2 b^2 r^2 - 2 b^6 - 6 b^4 r^2) x^4y^2 +\\ (- 2 a^6 + 2 a^4 b^2 - 6 a^4 r^2 - 6 a^2 b^4 + 2 a^2 b^2 r^2 - 2 b^4 r^2) x^2y^4 +\\ (2 a^6 - 4 a^4 b^2 - 4 a^4 r^2 + 2 a^2 b^2 r^2) y^6 + \\ (6 a^4 b^4 - 6 a^4 b^2 r^2 + a^4 r^4 - 6 a^2 b^6 + 10 a^2 b^4 r^2 -\\ \qquad 6 a^2 b^2 r^4 + b^8 - 6 b^6 r^2 + 6 b^4 r^4) x^4 +\\ (6 a^6 b^2 + 4 a^6 r^2 - 10 a^4 b^4 - 6 a^4 b^2 r^2 + 6 a^4 r^4 +\\ \qquad 6 a^2 b^6 - 6 a^2 b^4 r^2 - 10 a^2 b^2 r^4 + 4 b^6 r^2 + 6 b^4 r^4) x^2y^2 +\\ (a^8 - 6 a^6 b^2 - 6 a^6 r^2 + 6 a^4 b^4 + 10 a^4 b^2 r^2 +\\ \qquad 6 a^4 r^4 - 6 a^2 b^4 r^2 - 6 a^2 b^2 r^4 + b^4 r^4) y^4 +\\ (- 4 a^6 b^4 + 6 a^6 b^2 r^2 - 2 a^6 r^4 + 6 a^4 b^6 - \\ \qquad 8 a^4 b^4 r^2 + 4 a^4 b^2 r^4 - 2 a^4 r^6 - 2 a^2 b^8 + \\ \qquad 4 a^2 b^6 r^2 - 8 a^2 b^4 r^4 + 6 a^2 b^2 r^6 - 2 b^8 r^2 +\\ \qquad 6 b^6 r^4 - 4 b^4 r^6) x^2 +\\ (- 2 a^8 b^2 - 2 a^8 r^2 + 6 a^6 b^4 + 4 a^6 b^2 r^2 +\\ \qquad 6 a^6 r^4 - 4 a^4 b^6 - 8 a^4 b^4 r^2 - 8 a^4 b^2 r^4 -\\ \qquad 4 a^4 r^6 + 6 a^2 b^6 r^2 + 4 a^2 b^4 r^4 + 6 a^2 b^2 r^6 -\\ \qquad 2 b^6 r^4 - 2 b^4 r^6) y^2 +\\ (a^8 b^4 - 2 a^8 b^2 r^2 + a^8 r^4 - 2 a^6 b^6 + \\ \qquad 2 a^6 b^4 r^2 + 2 a^6 b^2 r^4 - 2 a^6 r^6 + a^4 b^8 +\\ \qquad 2 a^4 b^6 r^2 - 6 a^4 b^4 r^4 + 2 a^4 b^2 r^6 + a^4 r^8 -\\ \qquad 2 a^2 b^8 r^2 + 2 a^2 b^6 r^4 + 2 a^2 b^4 r^6 - 2 a^2 b^2 r^8 +\\ \qquad b^8 r^4 - 2 b^6 r^6 + b^4 r^8) = 0 \end{array}$

由于对根号平方的过程中已经去除了内外的方向信息，所以在椭圆内侧和外侧滚动的圆心形成的轨迹都是上面曲线的分支。注意到上面的曲线是不可约的，所以两个分支从代数上是无法分离的。作为例子，下图画出了 $a=2,b=\sqrt3,r=1$ 时的曲线，此时带入得到方程为

$9x^8 + 42x^6y^2 - 102x^6 + 73x^4y^4 - 332x^4y^2 + 205x^4 + 56x^2y^6 - 338x^2y^4 + 250x^2y^2 - 148x^2 + 16y^8 - 104y^6 - 119y^4 + 24y^2 + 36 = 0$

曲线方程（可直接复制到 www.geogebra.org/calculator 绘制版）

9 x^8 + 42 x^6 y^2 - 102 x^6 + 73 x^4 y^4 - 332 x^4 y^2 + 205 x^4 + 56 x^2 y^6 - 338 x^2 y^4 + 250 x^2 y^2 - 148 x^2 + 16y^8 - 104 y^6 - 119 y^4 + 24 y^2 + 36 = 0

绘制出来的图像长这样

x²/4 + y²/3 = 1 的椭圆和 r=1 的圆

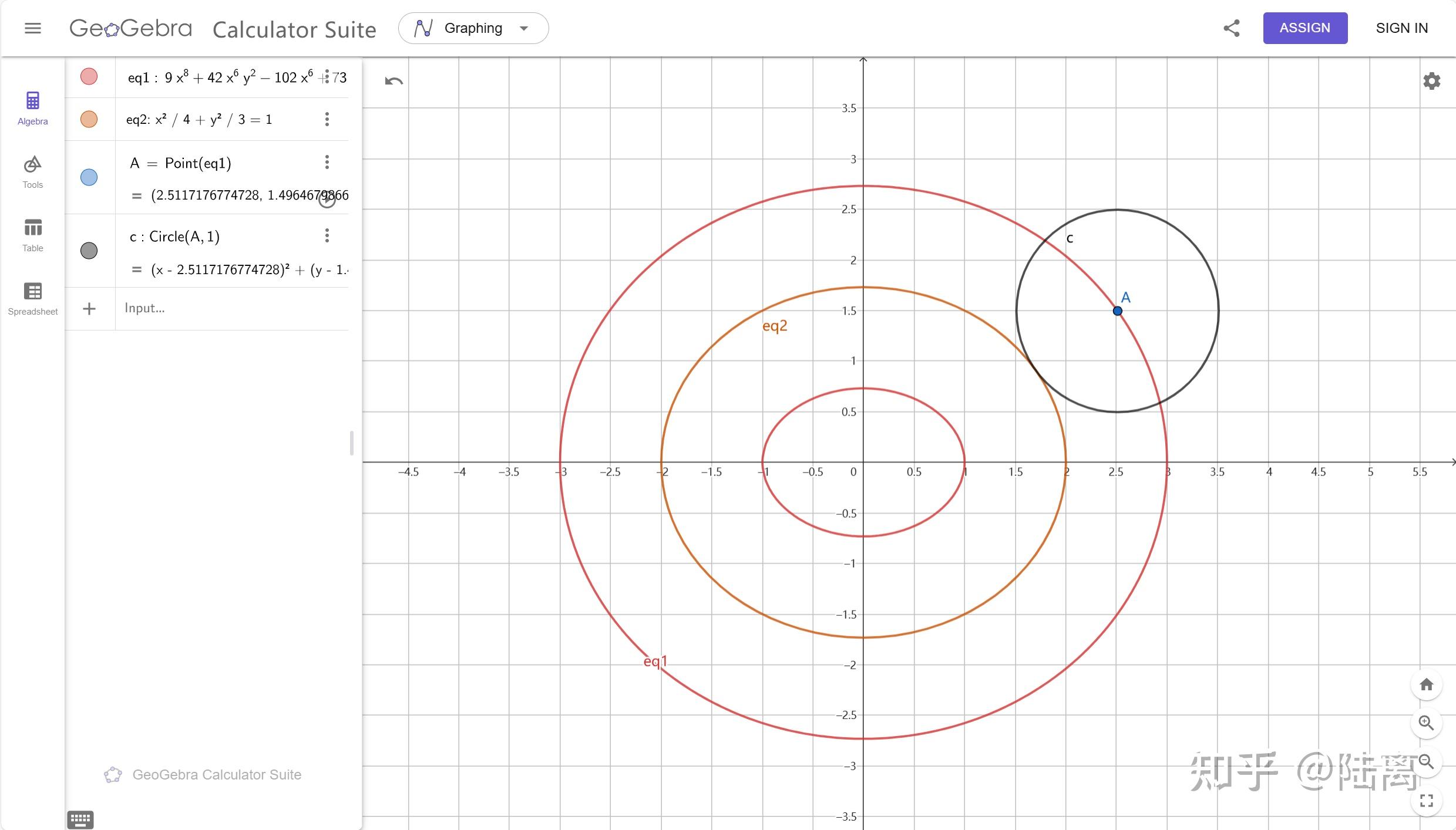
是符合预期的，其中外面一圈是内切，里面的一圈是内切，确实是两个分支

当椭圆长轴两端的曲率半径小于圆的曲率半径时在实平面上就会出现奇点，例如对 $a=\sqrt2,b=1,r=1$ 时顶端的曲率半径为 $b^2/a=1/\sqrt2 <1$ ，这时曲线方程为

$x^8 + 6 x^6 y^2 - 6 x^6 + 13 x^4 y^4 - 32 x^4 y^2 + x^4 + 12 x^2 y^6 - 42 x^2 y^4 + 30 x^2 y^2 + 4 y^8 - 12 y^6 - 15 y^4 - 4 y^2 = 0$

（可直接复制粘贴到 Geogebra 版）

x^8 + 6 x^6 y^2 - 6 x^6 + 13 x^4 y^4 - 32 x^4 y^2 + x^4 + 12 x^2 y^6 - 42 x^2 y^4 + 30 x^2 y^2 + 4 y^8 - 12 y^6 - 15 y^4 - 4 y^2

绘制出的图像如图：

x²/2 + y² = 1 的椭圆和 r=1 的圆

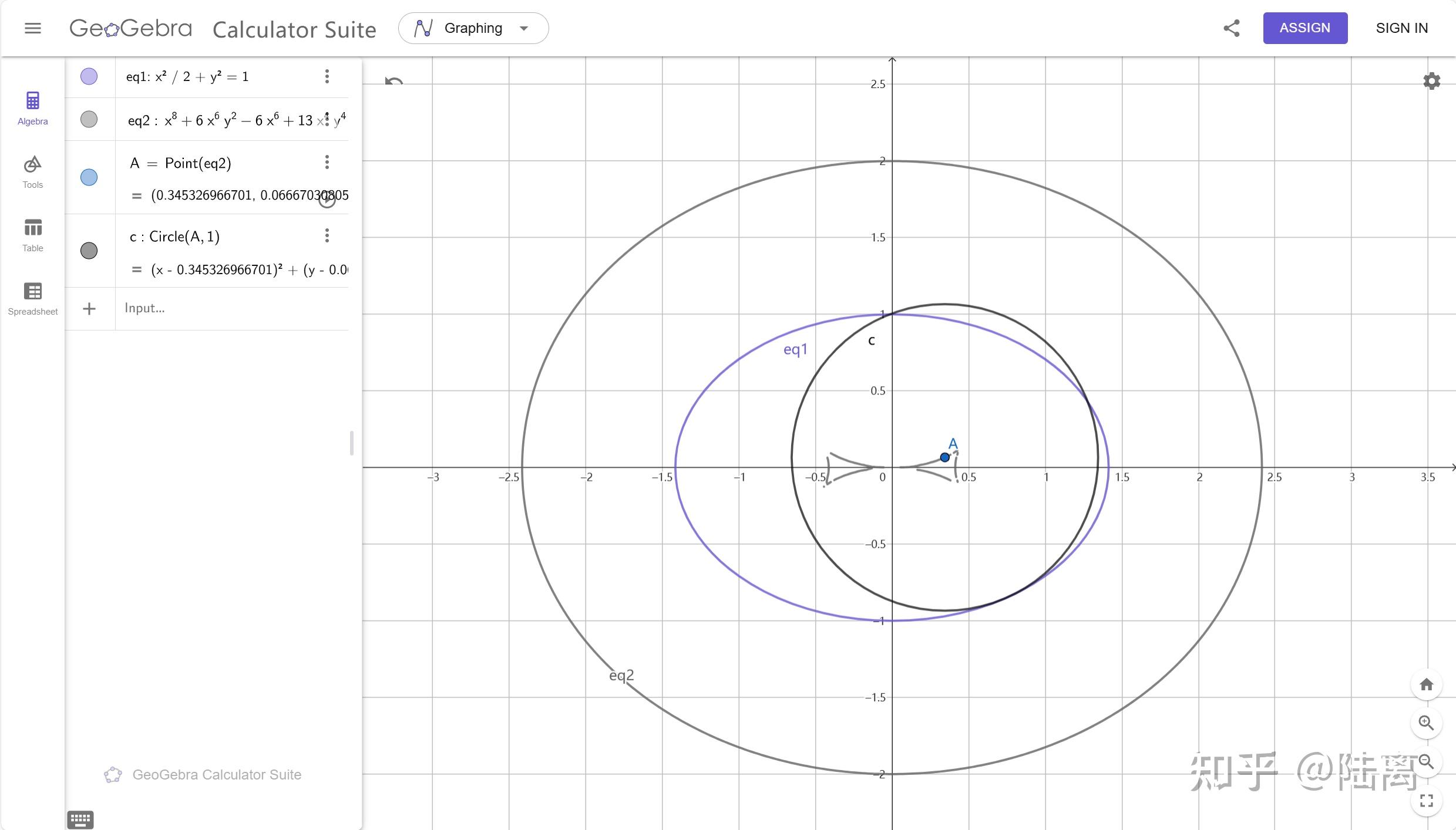
这时轨迹上的点并不能保证圆不与椭圆相交，因为方程仅仅给出了相切条件，而不包含不交条件，如果要解决这一问题需要引入额外的不等式约束。这里就暂时不做计算了。

最后，为了方便计算，这里放一个 python 代码来计算和椭圆相切的圆圆心走过的轨迹方程

import sympy a, b, r, x, y = sympy.symbols("a,b,r,x,y") polynomial = b**4*x**8 + (2*a**2*b**2 + 2*b**4)*x**6*y**2 +\ (-4*a**2*b**4 + 2*a**2*b**2*r**2 + 2*b**6 - 4*b**4*r**2)*x**6 +\ (a**4 + 4*a**2*b**2 + b**4)*x**4*y**4 +\ (-6*a**4*b**2 - 2*a**4*r**2 + 2*a**2*b**4 + 2*a**2*b**2*r**2 - 2*b**6 - 6*b**4*r**2)*x**4*y**2 +\ (6*a**4*b**4 - 6*a**4*b**2*r**2 + a**4*r**4 - 6*a**2*b**6 + 10*a**2*b**4*r**2 - 6*a**2*b**2*r**4 +\ b**8 - 6*b**6*r**2 + 6*b**4*r**4)*x**4 +\ (2*a**4 + 2*a**2*b**2)*x**2*y**6 +\ (-2*a**6 + 2*a**4*b**2 - 6*a**4*r**2 - 6*a**2*b**4 + 2*a**2*b**2*r**2 - 2*b**4*r**2)*x**2*y**4 +\ (6*a**6*b**2 + 4*a**6*r**2 - 10*a**4*b**4 - 6*a**4*b**2*r**2 + 6*a**4*r**4 + 6*a**2*b**6 -\ 6*a**2*b**4*r**2 - 10*a**2*b**2*r**4 + 4*b**6*r**2 + 6*b**4*r**4)*x**2*y**2 +\ (-4*a**6*b**4 + 6*a**6*b**2*r**2 - 2*a**6*r**4 + 6*a**4*b**6 - 8*a**4*b**4*r**2 +\ 4*a**4*b**2*r**4 - 2*a**4*r**6 - 2*a**2*b**8 + 4*a**2*b**6*r**2 - 8*a**2*b**4*r**4 +\ 6*a**2*b**2*r**6 - 2*b**8*r**2 + 6*b**6*r**4 - 4*b**4*r**6)*x**2 +\ a**4*y**8 + (2*a**6 - 4*a**4*b**2 - 4*a**4*r**2 + 2*a**2*b**2*r**2)*y**6 +\ (a**8 - 6*a**6*b**2 - 6*a**6*r**2 + 6*a**4*b**4 + 10*a**4*b**2*r**2 + 6*a**4*r**4 -\ 6*a**2*b**4*r**2 - 6*a**2*b**2*r**4 + b**4*r**4)*y**4 +\ (-2*a**8*b**2 - 2*a**8*r**2 + 6*a**6*b**4 + 4*a**6*b**2*r**2 + 6*a**6*r**4 - 4*a**4*b**6 -\ 8*a**4*b**4*r**2 - 8*a**4*b**2*r**4 - 4*a**4*r**6 + 6*a**2*b**6*r**2 + 4*a**2*b**4*r**4 +\ 6*a**2*b**2*r**6 - 2*b**6*r**4 - 2*b**4*r**6)*y**2 +\ (a**8*b**4 - 2*a**8*b**2*r**2 + a**8*r**4 - 2*a**6*b**6 + 2*a**6*b**4*r**2 + 2*a**6*b**2*r**4 -\ 2*a**6*r**6 + a**4*b**8 + 2*a**4*b**6*r**2 - 6*a**4*b**4*r**4 + 2*a**4*b**2*r**6 + a**4*r**8 -\ 2*a**2*b**8*r**2 + 2*a**2*b**6*r**4 + 2*a**2*b**4*r**6 - 2*a**2*b**2*r**8 + b**8*r**4 -\ 2*b**6*r**6 + b**4*r**8) def center_trajectory(a_value, b_value, r_value): """ Return the trajectory of a circle with radius r_value rolling along x^2 / a^2 + y^2 / b^2 = 1 Example: >>> center_trajectory(2, sympy.sqrt(3), 1) 9 x^8 + 42 x^6 y^2 - 102 x^6 + 73 x^4 y^4 - 332 x^4 y^2 + 205 x^4 + 56 x^2 y^6 - 338 x^2 y^4 + 250 x^2 y^2 - 148 x^2 + 16 y^8 - 104 y^6 - 119 y^4 + 24 y^2 + 36 """ print(str(polynomial.subs({ a: a_value b: b_value r: r_value })).replace("**", "^").replace("*", " "))

上一篇：如何看待东海道新干线决定将Nozomi的自由席比例降低为9：1？

下一篇：关于冯骥在微博中所说的“路还很长，风还很邪，妖王还很狂妄，但我们一直在变强”，大家有什么看法？

END