为什么（x+a）/（x^2+bx+c）的三个拐点总是共线？

这其实是一个古典代数几何的问题：三次曲线的任何两个拐点连线，与曲线的第三个交点总是另一个拐点。

考虑三次曲线 ，取两个拐点 ，设 连线 再次交三次曲线于 ，设 处的切线依次为 。根据拐点的定义（切线与曲线有三重交点），由于 与 交于 九个点，而 与 交于 八个点，二者的第九个交点必须也是 ，也就是说 与 的交点是三重的，即 也是拐点。

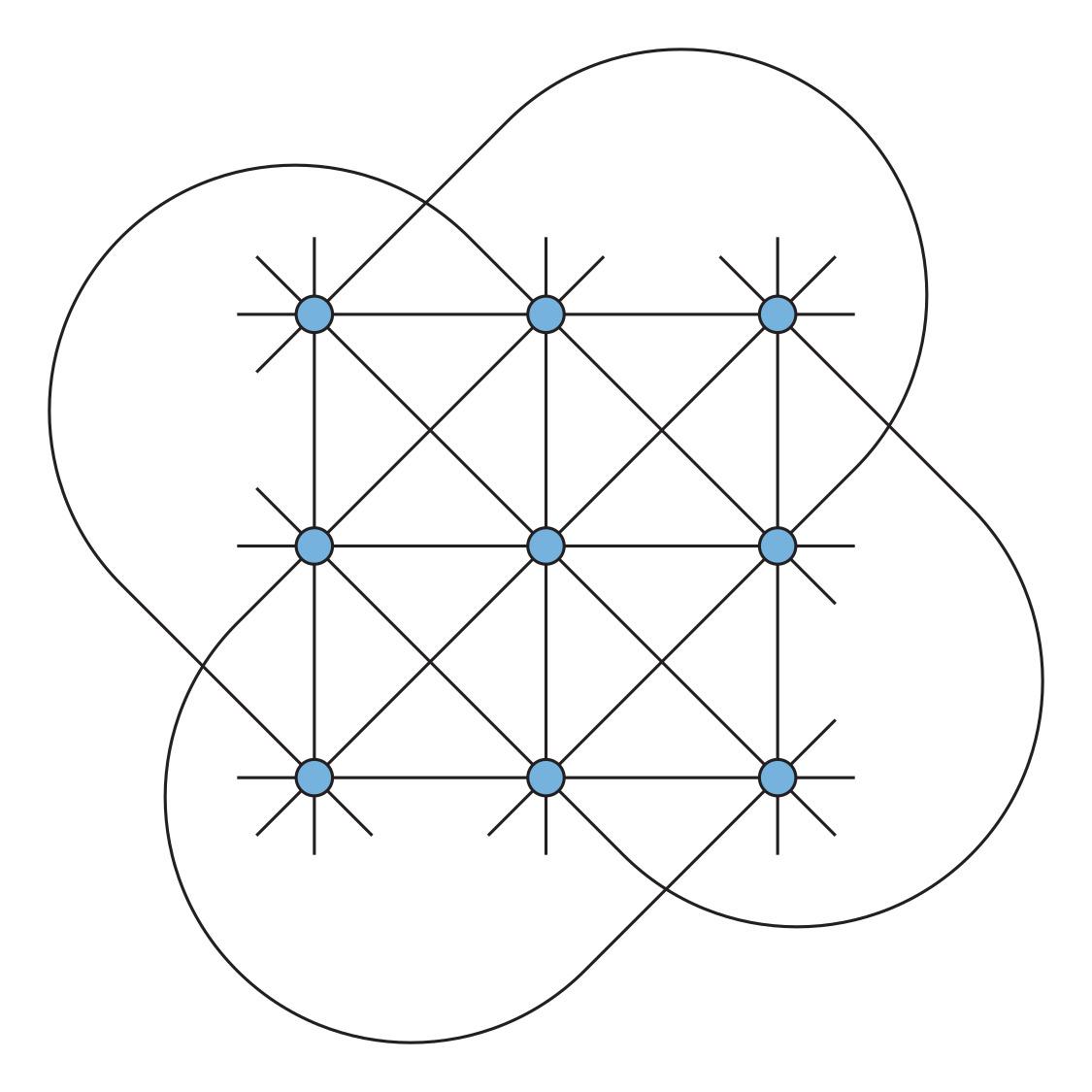
多说一句，一般的三次曲线会有九个拐点，任何两个的连线都经过第三个，最终这九个交点会形成 的结构，这也被称为 Hesse 构型。别看它在平面上不可能实现，但在复射影平面上确实是可以做到的。