将筷子斜插入碗中，为什么碗壁上会出现类似双曲线的图案？

题主的观察非常细致，适度简化模型，这个问题可以用中学知识解决，且计算结果确实是非常漂亮的双曲线！

碗-筷子模型

碗可以近似成凹柱面镜，筷子近似为方向指向镜面外斜上方的直线：

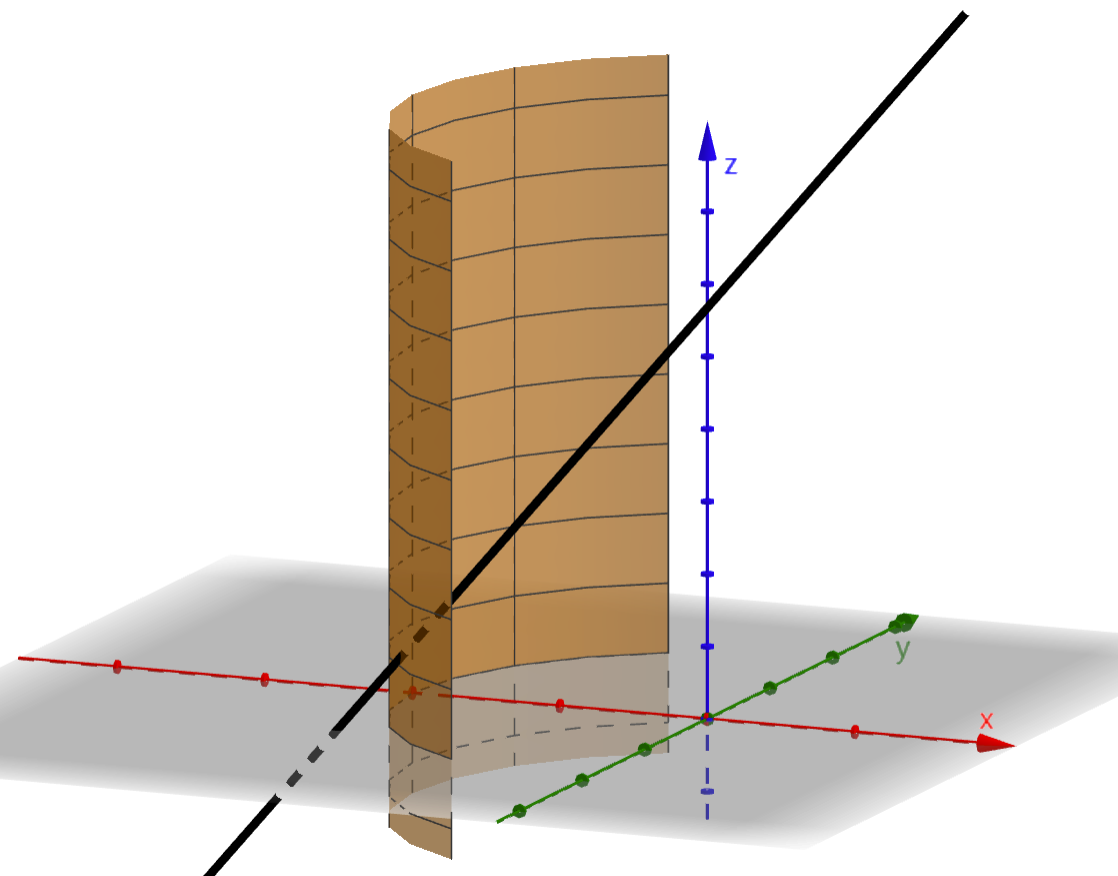
筷子落在 的平面内且z关于x线性增加，且题主视频所示移动过程就是y的常数值从负半轴向正半轴变化的过程。俯视图如下：

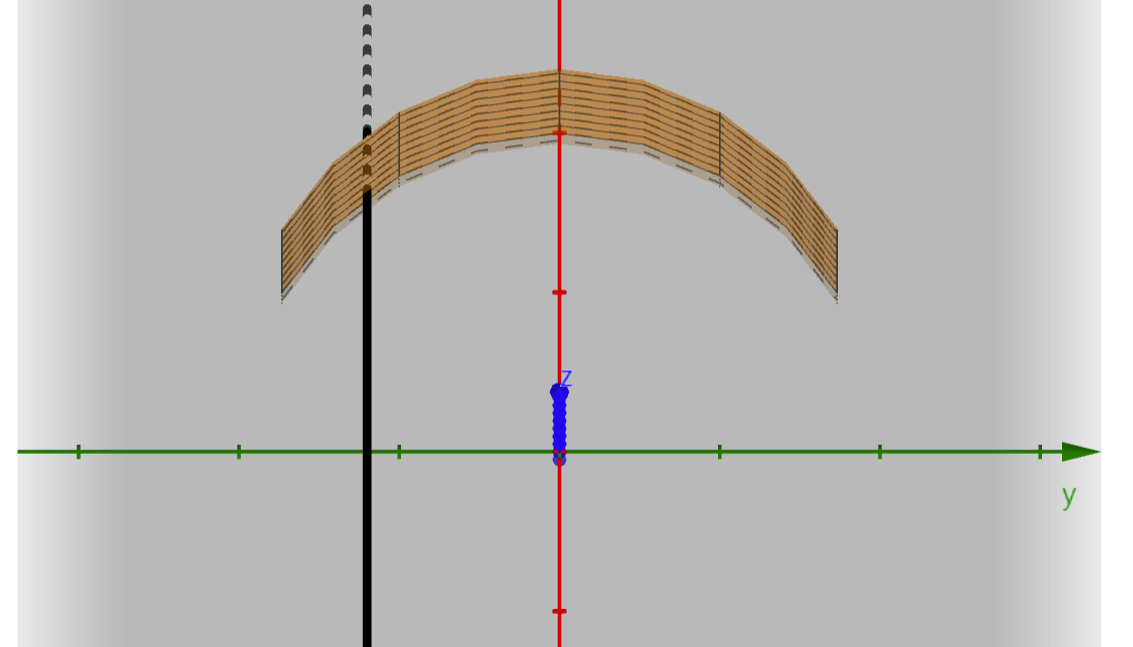
那么我们想要得到的是沿着x轴看去，筷子的像在yz平面上的投影是双曲线。

筷子任意点与其像点有相等的 值，故只需要计算每个 的水平截面上，筷子在该水平截面内的点 关于凹面镜的像点的 值即可，得到一个像点y值关于z值的函数关系，我们期望这个函数图像是双曲线。

为了计算y值，我们需要回忆凹面镜成像的基本知识。

凹面镜的高斯成像方程

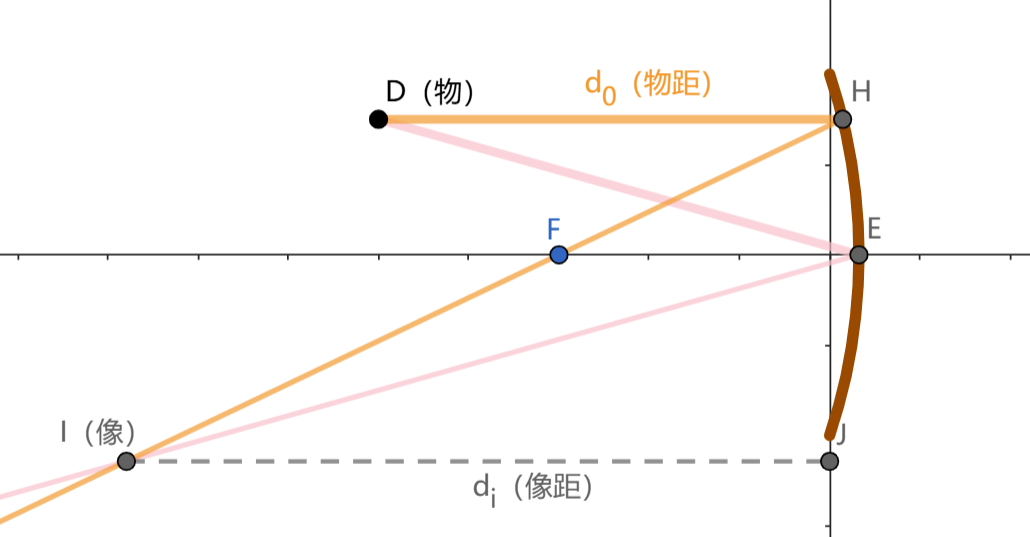
下图是一个水平剖面图，D是筷子上的点，F是凹面镜的焦点。

• 粗橙线是从D发出的水平光线，按成像原理其反射光线（细橙）穿过焦点。
• 粗粉线是从D射向镜面对称中心的光线，按对称性其反射光线（细粉）关于x轴与其完全对称。
• 两反射光线的交点就是像点。物距和像距的定义参看下图。注意 就是上节定义的 。

这里考虑的是物距大于焦距的情形。

• 先考虑 和 的数量关系。设焦距（线段 的长度）为 。近似把凹面镜看成平的，也就是H、E、J大致都在y轴，也都在凹面镜上。
• 由光路可逆，反射光线JI的入射光线为DJ应当穿过焦点，因此D、F、J是共线的。
• 考虑如下相似形

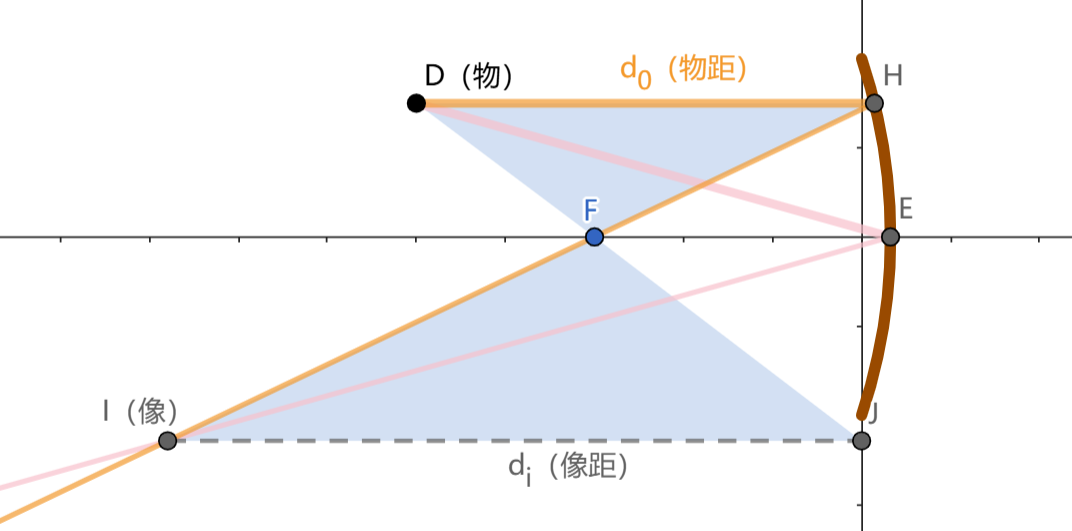
可以得到著名的高斯镜面方程：

也不难发现，像点的y值的绝对值 与物点的y值 的比例正是像距与物距的比例。

而 是 的线性函数，可设为 ，整理有

不难发现 与 是双曲关系。

当物距小于焦距时结论完全类似。参见下图，读者可以自行完成证明。

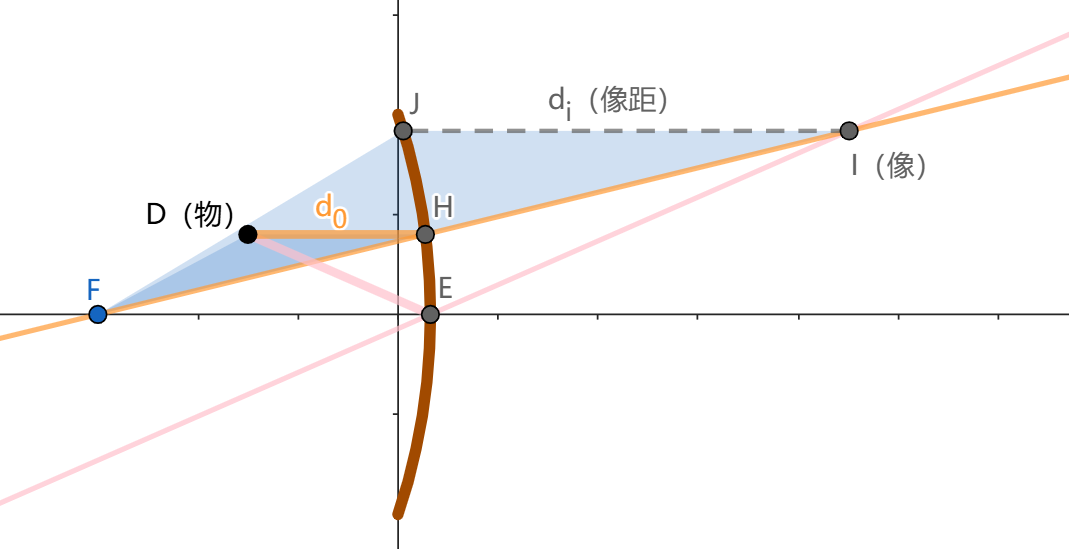
在上图中我不得不将 减小以保证我们的近似（凹面镜和y轴几乎重合）不至于失效太多。由此也可看出，当 较大时我们的计算会产生较大的误差，实际曲线因此会偏离双曲线。

题主视频中的过程即是 从负变正，根据上式确定的双曲线的形状也会因此发生变化。感兴趣的读者可以据此详细探讨视频中形状的动态变化，这里限于篇幅就不再展开了。