 "函数"搜索结果 10 条
"函数"搜索结果 10 条如何优雅的求∫ Inx dx 的原函数?
那么我们还是不知道 [公式] 的原函数是什么我们甚至不知道 [公式] 是什么于是,我们先给个符号,省点墨水 [公式] 虽然我们知道的东西并不多 但是,我们却不争气地知道 [公式] 于是,我们就得到了 [公式] 整理一下就是 [公式] 接下来,我们两边同时积分 [公式]
请问Python中,为什么read是一个函数,而write是一个方法?
古代语言里把子程序分为两类。有返回值的叫“函数”,没有返回值的叫“过程”(比如 Basic 里的 Sub 和 Pascal 里的 Procedure)。一般来说,调用“函数”是为了获取返回值,而调用“过程”是为了产生某种副作用。 现代语言一般合并两者,统称为“函数”,因为是否有返回值其实并不重要,不足以用来区分两个不同的概念,也没有必要占用两个不同的关键字。但这里的“函数”只是用来指代“子程序”而已,并不是数学上的“映射”。 …
为什么人可以一眼看出函数的全局最小值,而计算机不能?
《概念神之我能一眼看出函数的极值》 厨子有厨子的才能,国王有国王的才能。 人各有天赋,莫扎特会谱曲、梵高会画画。而我的天赋是,能 一眼看出函数的极值。 这实在是一个很不够直观的天赋,特别是因为我其他部分的脑子还只是一个堪堪够用的普通人程度。回忆我所剩无几的孩提时代记忆,似乎这个天赋一开始的体现,是我能够一眼看出抛出的球会在哪里达到最高点;看出星星和月亮在天空的轨迹;但这些事情看起来实在是平平无奇,彼…
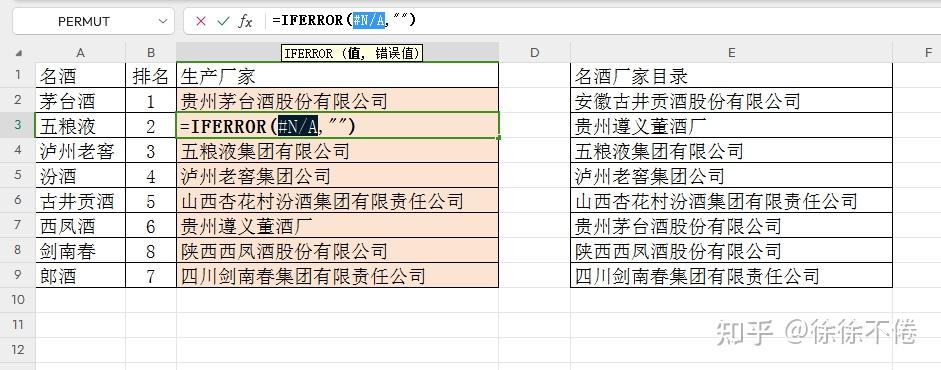
请问用Lookup,find,if error函数根据名酒的名字,查找出生产厂家?
公式写错了、逻辑混乱,不仅C3单元格是空白,下面的几个结果的对应关系也都是错误的。 所以,单独分析“为什么是空白”也没什么意义(不过,这一部分我还是放在最后了)。 1、公式修改 A列改为引用一个目标值,E列改为整列有效数据。 2、示例公式 =IFERROR(LOOKUP(1,0/FIND(A2,E$2:E$9),E$2:E$9),"") *公式中有相对引用和锁定行号的混合引用,输入时要注意。 3、其它思路 如果不限定LOOKUP和FIND函数,可以把LOOKUP函数换为VLO…
存不存在填充整个平面的函数?
存在的,可以参考 Cauchy's functional equation 具体来讲,如果一个函数 [公式] 满足 [公式] ,那么就说f是Cauchy函数方程的解,这个方程显然的解是正比例函数 [公式] ,但是这个方程存在其他的非连续解,并且任何一个非连续解的函数图像都在整个平面上稠密只需要考虑 [公式] 作为 [公式] -线性空间的一组Hamel basis [公式] ,设 [公式]
函数(function)这个词的翻译是否精准?
翻译地棒极了,因为翻译地狗屁不通。是这样的,越是抽象的数学概念,就越是应该翻译的狗屁不通,这样才棒,这样才不会因为和现实事物发生错误映射而产生误解,才有利于理解。如果比喻地翻译成了现实中的事物,初学者就会在想起这个抽象概念时永远先想起那个不恰当的比喻,永远带着拐杖走路。 函数二字是古语,对现代人已经没有任何具体含义了,如此正好,用来对应数学名词。抽象科学概念的命名本身就应该足够抽象,最好不要顾名…
有没有符合f'(x)=f(x+1)的函数?
这种牵扯时频域分析的,直接拉普拉斯变换就好了 应该是个标准正弦函数 -------------------------------------------分割线-------------------------------------------------- 对不起我错了,拉普拉斯变换我没办法求出来= =,但是否有还是存疑 设拉普拉斯变换对 [公式] 考虑简单情况下的双边拉普拉斯变换,根据时域微分定理和时域移动定理 [公式] [公式] 则可以同时对两边进行拉普拉斯变换…
我好像发现了一个有关三角函数的定理,如何证明?
这里给出一种解释,具体的值我还没有计算出来. 下面证明当素数 [公式] 时, [公式] 其中 [公式] ,且 [公式] ,换句话说, [公式] 是二次域 [公式] 中的代数整数,且模(norm)是 [公式] .对于题主给出的 [公式] ,都有 [公式] ,当 [公式] 时, [公式] 当 [公式] 时, [公式]
高一开学,同学在讨论偏导函数、四阶导数,我该怎么办?
这什么菜鸡高中。 我们高一开学的时候,同学们讨论的话题都是,如何绕开Fatou引理来证明Lebesgue控制收敛定理,或者,在什么条件下有界变差函数可以加强为绝对连续函数甚至是Lipschitz函数。学霸们组成的小圈子则在讨论Noetherian module和Artinian module之间的区别和联系,或者准备第二天课上要讲的Nakayama引理。 开学第二周,不知道是谁刺探的消息,说隔壁班已经开始讲Riemann zeta函数,这让我们这群只会证明Liouville定理…
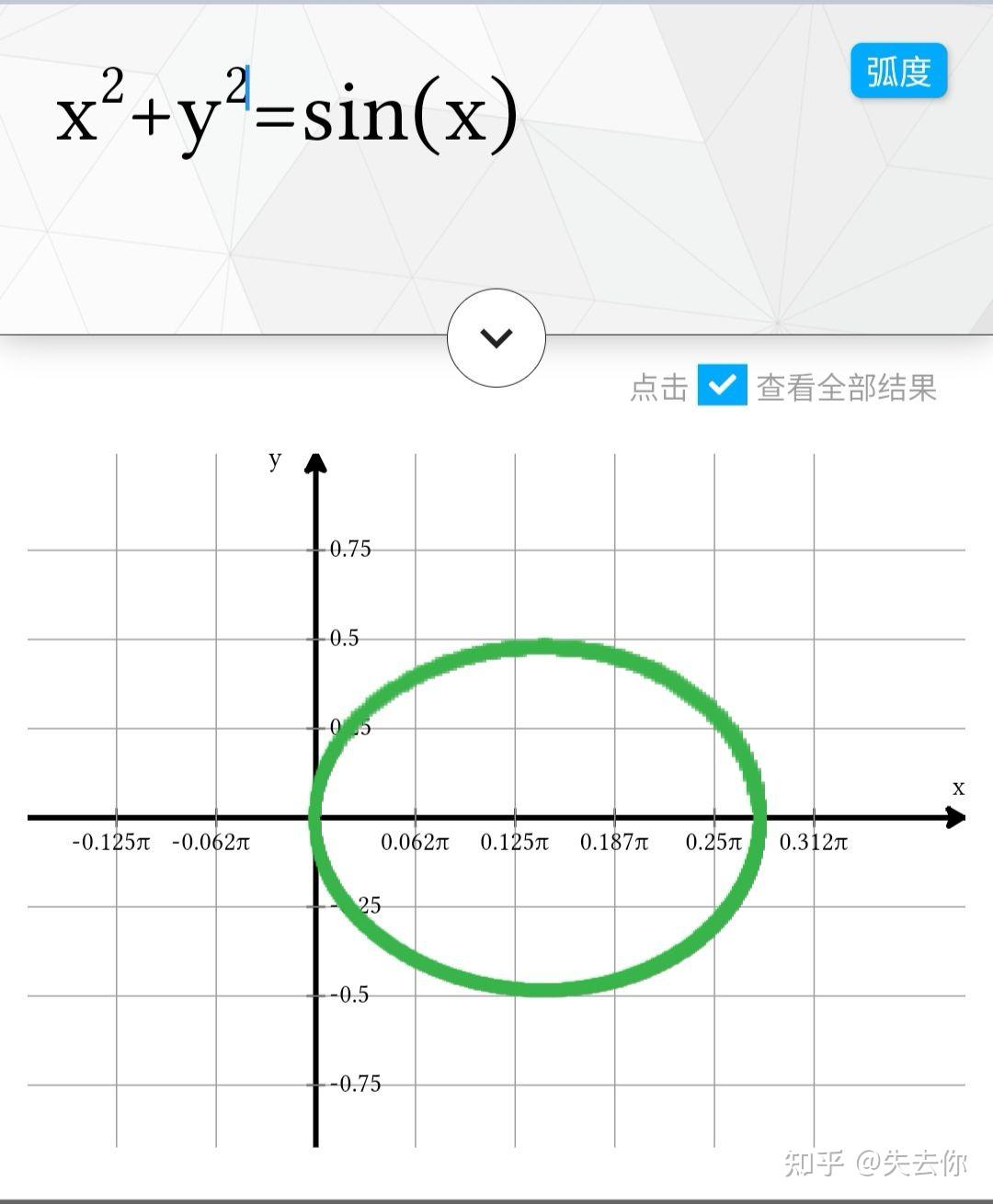
此函数图像是否为椭圆?
不是椭圆。 至于为什么不是椭圆,因为不满足椭圆定义。 但是我猜题主想问的是图形为什么和椭圆如此相似。 只能说是巧合。 但为什么是巧合,我也回答不了。 又但是,偶然必包含必然。 和椭圆如此相似肯定是有原因的 。 再但是,原因在哪里,目前我还不知道。 说不定我再想想就明白了。 这个也长的像椭圆,y^2改成y以后长的也像抛物线。